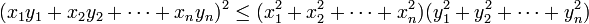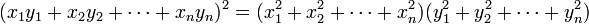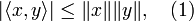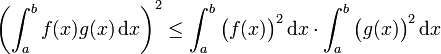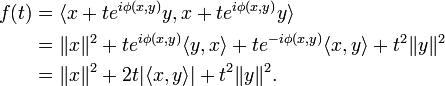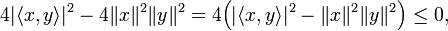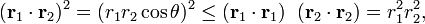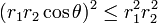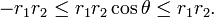Cauchy-Schwarz inequality
In mathematics, the Cauchy-Schwarz inequality is a fundamental and ubiquitously used inequality that relates the absolute value of the inner product of two elements of an inner product space with the magnitude of the two said vectors. It is named in the honor of the French mathematician Augustin-Louis Cauchy and German mathematician Hermann Amandus Schwarz.
Contents |
[edit] The inequality for real numbers
The simplest form of the inequality, and the first one considered historically, states that
for all real numbers x1, …, xn, y1, …, yn (where n is a arbitrary positive integer). Furthermore, the inequality is in fact an equality
if and only if there is a number C such that xi = Cyi for all i.
[edit] The inequality for inner product spaces
Let V be a complex inner product space with inner product  . Then for any two elements
. Then for any two elements 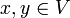 it holds that
it holds that
where 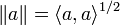 for all
for all 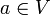 . Furthermore, the equality in (1) holds if and only if the vectors x and y are linearly dependent (in this case proportional one to the other).
. Furthermore, the equality in (1) holds if and only if the vectors x and y are linearly dependent (in this case proportional one to the other).
If V is the Euclidean space Rn, whose inner product is defined by
then (1) yields the inequality for real numbers mentioned in the previous section.
Another important example is where V is the space L2([a, b]). In this case, the Cauchy-Schwarz inequality states that
for all real functions f and g in ![\scriptstyle L^2([a,b])](../w/images/math/8/6/3/86339d3517656b34a9b22fff2002c44f.png) .
.
[edit] Proof of the inequality
A standard yet clever idea for a proof of the Cauchy-Schwarz inequality for inner product spaces is to exploit the fact that the inner product induces a quadratic form on V. Let x,y be some fixed pair of vectors in V and let 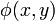 be the argument of the complex number
be the argument of the complex number 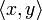 . Now, consider the expression
. Now, consider the expression 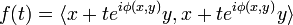 for any real number t and notice that, by the properties of a complex inner product, f is a quadratic function of t. Moreover, f is non-negative definite:
for any real number t and notice that, by the properties of a complex inner product, f is a quadratic function of t. Moreover, f is non-negative definite: 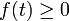 for all t. Expanding the expression for f gives the following:
for all t. Expanding the expression for f gives the following:
Since f is a non-negative definite quadratic function of t, it follows that the discriminant of f is non-positive definite. That is,
from which (1) follows immediately.
[edit] Application in ℝ3
For vectors r1 and r2 in ℝ3 it holds that
where r1 = ||r1|| and r2 = ||r2|| are the lengths of the two vectors; θ is the angle between them. Taking square roots of
gives
Hence the Cauchy-Schwarz inequality in ℝ3 is equivalent to stating that −1 ≤ cos θ ≤ 1. The equalities follow when θ = 0 and θ = π, for which cosθ = 1 and cosθ = −1, respectively. Hence, equality holds only for the case that the two vectors are parallel (θ = 0) or antiparallel (θ = π).
[edit] References
| |
Some content on this page may previously have appeared on Citizendium. |