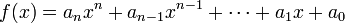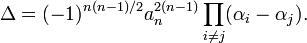Discriminant of a polynomial

From Knowino

Jump to: navigation, search

In algebra, the discriminant of a polynomial is an invariant which determines whether or not a polynomial has repeated roots.

Given a polynomial

$f(x)= a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0$

with roots 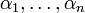$\alpha_1,\ldots,\alpha_n$ , the discriminant Δ(f) is defined as

$\Delta = (-1)^{n(n-1)/2} a_n^{2(n-1)} \prod_{i \neq j} (\alpha_i - \alpha_j) .$

The discriminant is thus zero if and only if f has a repeated root.

In spite of the definition in terms of the roots, Δ(f) appears to be a polynomial function of the coefficients 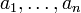$a_1,\ldots,a_n$ and may be obtained as the resultant of the polynomial and its formal derivative.

[edit] Examples

The discriminant of a quadratic $a X 2 + b X + c$ is $b 2 - 4 a c$ , which plays a key part in the solution of the quadratic equation.

[edit] References

Serge Lang (1993). Algebra, 3rd ed. Addison-Wesley, 193-194,204-205,325-326. ISBN 0-201-55540-9.

Some content on this page may previously have appeared on Citizendium.

Discriminant of a polynomial

[edit] Examples

[edit] References

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox