Inner product space
From Knowino
In mathematics, an inner product space is a vector space that is endowed with an inner product. It is also a normed space since an inner product induces a norm on the vector space on which it is defined. A complete inner product space is called a Hilbert space.
[edit] Examples of inner product spaces
- The Euclidean space ℝn endowed with the real inner product
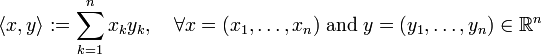 .
.
- This inner product induces the Euclidean norm ||x|| = ⟨ x, x ⟩½.
- The space
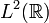 of the equivalence classes of all complex-valued Lebesgue measurable scalar square integrable functions on ℝ with the complex inner product
of the equivalence classes of all complex-valued Lebesgue measurable scalar square integrable functions on ℝ with the complex inner product
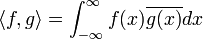 .
.
- Here a square integrable function is any function f satisfying
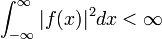 .
.
- The inner product induces the norm
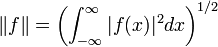
| |
Some content on this page may previously have appeared on Citizendium. |

