Chemical Physics

Theoretical background

Introduction

In this experiment we shall address electrical conduction through aqueous solutions. Although water is itself a very poor conductor of electricity, the presence of ionic species in solution increases its conductance considerably. The conductance of such electrolytic solutions depends upon the concentration of the ions present and their natures (through their charges and mobilities).

Conductance behavior as a function of concentration differs for strong and weak electrolytes respectively. In this experiment, we will study both strong and weak electrolytes, at a number of dilute concentrations. The acid dissociation constant (also called acidity constant or acid-ionization constant) for a weak electrolyte will be calculated from the data obtained.

Electrolyte solutions obey Ohm’s law just as metallic conductors do. Thus the current, I, passing through a given body of solution, is proportional to the applied potential difference, V. The resistance, R, of the body of solution in ohms (Ω) is given by R = V/I, where the potential difference is expressed in volts, and the current in amperes. The conductance, defined as the reciprocal of the resistance, of a homogeneous body of uniform cross-section, is proportional to the cross-sectional area A and inversely proportional to the length ℓ, such that:

$${1\over R} = {{κ ·A} \over l}$$

Where κ is the specific conductance with units Ω^-1·m^-1 (By international agreement, the reciprocal ohm Ω^-1 is now called a Siemens, S=1Ω^-1). One can think of the specific conductance as the conductance of a cube of material, 1 m on each edge. As it is difficult to build a cell with well defined geometrical parameters A and ℓ, any cell should be calibrated with a solution of exactly known specific conductance. From equation (1), we can determine the cell constant K:

$$ K ≡ {l \over A} = κ ·R $$

The cell constant, K, with units cm^-1, is determined by measuring the resistance of a cell filled with a solution of known specific conductance, which is here KCl. Once the cell constant K has been determined, specific conductances of any solution can be calculated from experimental resistances using equation (2). The specific conductance κ increases as the concentration increases. A more fundamental unit of electrolytic conductance is the equivalent conductance Λ, which can be thought of as the value of κ contributed by one equivalent of ions contained in 1000 cm³ (1 Liter) of solvent. It is defined as:

$$ Λ = {1000 ·κ \over C} $$

The units of concentration, c, are equiv/L; and the units of Λ are cm²·equiv^-1·ohm^-1. This is a CGS unit, and is the unit of equivalent conductance most frequently tabulated in the literature. The SI unit is obtained by multiplying the CGS unit by 10^-4. Note, that in the case of simple one-one electrolytes A⁺B^-, there is no distinction between equivalents and moles, and the equivalent conductance is the same as the molar conductance.

Strong Electrolytes

A strong electrolyte is a solute that completely, or almost completely, ionizes or dissociates in a solution. While a given solution’s specific conductance increases with concentration, its equivalent conductance decreases as the concentration increases. Onsager showed theoretically for strong electrolytes in dilute solution, that the effect of ionic attraction reduces the equivalent conductance.

$$ Λ = {Λ_0 - A · C^{1/2}} $$

Below concentrations of about 0.1M, a plot of Λ against c^½ gives a straight line, the intercept of which equals Λ₀, or the equivalent conductance at infinite dilution. At infinite dilution the ions act completely independently, and it is then possible to express Λ₀ as the sum of the limiting conductances of the separate ions. For a one-one electrolyte A⁺B^-

$$ Λ_0 = λ_0^+ + λ_0^- $$

Where Λ₀⁺=ℱ·U₀⁺ and Λ₀-=ℱ·U₀^-, ℱ is a Faraday number, and λ₀⁺ and λ₀^- are the ionic equivalent conductances of positive and negative ions respectively. Note that U is the mobility of the ion, defined as the speed of the ion under the influence of an electric field:

$$ U_0^± = {z^± ⋅ v \over E} $$

Where z⁺ and z^- are a valences of positive and negative ions respectively, and therefore the mobility has units of m²s^-1V^-1. A table of equivalent conductances at infinite dilution of some strong electrolytes is presented below:

Equivalent conductances at infinite dilution (cm² equiv^-1 ohm^-1) of some strong electrolytes
Electrolyte	Λ₀	Electrolyte	Λ₀
HCl	426.16	CaCl₂	135.84
LiCl	115.03	Ca(NO₃)₂	130.94
NaCl	126.45	BaCl₂	139.98
KCl	149.86	NaNO₃	121.55
KBr	151.90	KNO₃	144.96
NH₄CL	149.70	NaO₂CCH₃	91.00

Weak Electrolytes

For a weakly ionized substance, Λ varies much more markedly with concentration because the degree of ionization, α, varies strongly with concentration. The equivalent conductance, however, must approach a constant finite value at infinite dilution, Λ₀, which again corresponds to the sum of the limiting ionic conductances. It is usually impractical to determine this limiting value from extrapolation of Λ values obtained with the weak electrolyte itself, since to obtain an approach to complete ionization the concentration must be made too small for effective measurement of conductance. However, Λ₀ for a weak electrolyte can be deduced from Λ₀ values obtained for strong electrolytes by the use of equation (5). As an example, let us consider acetic acid (CH3COOH, denoted as HAc) as a typical weak electrolyte. It follows from equation (5) that:

$$Λ_0(HAc) = Λ_0(HX) + Λ_0(MAc) - Λ_0(MX)$$

Where M⁺ is any convenient univalent positive ion such as K⁺ or Na⁺ and X- is a univalent negative ion such as Cl- or Br-. The only restriction on M and X is the requirement that HX, MAc, and MX must all be strong electrolytes so that their Λ₀ values can be obtained by extrapolation using equation (4). For sufficiently weak electrolytes, the ionic concentration is small and the effect of ion attraction on the mobilities is slight; thus we may assume the mobilities to be independent of concentration and obtain the approximate expression:

$$α = {Λ \over Λ_0}$$

If one measures for a weak electrolyte at a concentration c and calculates Λ₀ from the conductivity data for strong electrolytes as described above, it is possible to obtain the degree of ionization of the weak electrolyte at concentration c.

Equilibrium Constant for Weak Electrolyte

Knowing the concentration c of the weak electrolyte, say HAc, and its degree of ionization α at that concentration, the concentrations of H⁺ and Ac^- ions and of un-ionized HAc can be calculated. Then the equilibrium constant in terms of concentrations Kc can be calculated from

$$K_C = {[H^+][Ac^-] \over [HAc]} = {C·α^2 \over 1-α}$$

Once we know Kc, we can predict the concentration dependence of the equivalent conductance. More usefully, we can use the concentration dependence of Λ in measurements of the limiting conductance. Using Equations (8) and (9) we obtain Ostwald’s law:

$${1 \over Λ} = {1 \over Λ_0} + {Λ · C \over K_C · Λ_0^2}$$

This equation implies that, if 1/Λ is plotted against Λ·c, then the intercept at c=0 will be 1/Λ₀.

Walden’s rule

Walden’s rule is the empirical observation that the product Λ⁰η, where η is a viscosity of the solution, is approximately constant for the same ions in different solvents. This rule can be derived in the following way. As the ion moves through the solvent, it experiences two forces: an electrical force, F_E=zeE, and a frictional force F_fr=6πrηv, where z, r and v are the valence, the radius and the velocity of the ion and E is the magnitude of the electric field. The two forces act in opposite directions, and the ions quickly reach a terminal speed, when the accelerating electrical force is balanced by the viscous drag:

$$zeE = 6πrηv$$

Taking into account that Λ₀∝v/E, equation (6) and (11) leads to Walden’s rule:

$$Λ_0η ≈ Constant$$

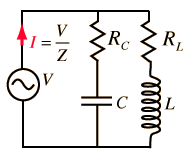
Reminder: RLC AC circuits

You are familiar with Ohm's law, describing the relations between current, voltage and resistance in a DC circuit. In an AC circuit Ohm's law takes a slightly different form:

$$I = {V \over Z}$$

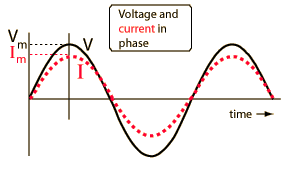
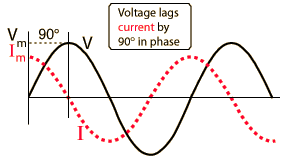
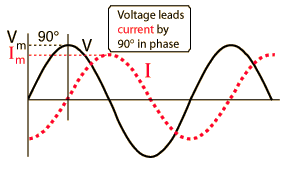
Where Z is the impedance, and the current and voltage receive their root-mean-square values. The contributions of capacitors and inductors to the impedance differ in their phase from the resistive components by 90°. The easiest way to symbolize this is by turning the impedance to a complex number. It is important to remember that the complex notation is just a representation, and the measured value is the absolute value of the impedance!

The impedance can be represented as:

$$Z = R + iX = |Z|e^{iφ}$$

Where R is the resistance of the component and X is its’ reactance; |Z| is the absolute value of the impedance (which is experimentally measured) and φ is the phase difference between the current and voltage in the circuit.

Generally, |Z| and φ can be calculated as:

$$|Z|= \sqrt{ R^2+X^2}$$

$$φ =arctan {X \over R}$$

The impedance contribution of each component is shown in the table below:

Impedance contribution of each electrical component
Component	Phase difference	Resistance (R)	Reactance (X)	Impedance (Z)
Resistor		R	0	R
Capacitor		0	$$-{1 \over ωC}$$	$$-{i \over ωC}$$
Inductor		0	$$ωL$$	$$iωL$$

When all the circuit's components are connected in series, the impedance is:

$$Z = \sum\limits_j Z_j = \sum\limits_j R_j + iX_j$$

When the components are connected in parallel, the impedance is:

$${1 \over Z} = \sum\limits_j {1 \over Z_j} = \sum\limits_j { 1 \over R_j + iX_j}$$

For exemple, the impedance of the circuit showen in figure 1 ,according to equations (14) and (17),is:

$${1 \over Z} = {1 \over Z_1} + {1 \over Z_2} \Rightarrow Z = {Z_1 ⋅ Z_2 \over Z_1 + Z_2} = {(R_1 - {i \over ωC}) ⋅ (R_2 + iωL) \over (R_1 - {i \over ωC}) + (R_2 + iωL)}$$