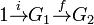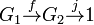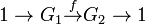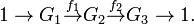Exact sequence

From Knowino

Jump to: navigation, search

In mathematics, particularly in abstract algebra and homological algebra, an exact sequence is a sequence of algebraic objects and morphisms which is used to describe or analyse algebraic structure. (See below for the formal definition.)

In general the concept of an exact sequence makes sense when dealing with algebraic structures for which there are the concepts of "objects", "morphisms" between objects and of "subobjects" attached to morphisms which play the role of "kernel" and "image".

We shall expound the concept in group theory: very similar remarks apply to module theory.

A sequence will simply be a collection of group homomorphisms $f i$ and groups $G i$ with 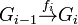$G_{i-1} \stackrel{f_i}{\rightarrow} G_i$ , indexed by some interval of the integers. A sequence will be termed exact at the term $G i$ if there are maps $f i - 1$ and $f i$ to the left and right of the term $G i$ and the condition that the kernel of $f i$ is equal to the image of $f i - 1$ holds. An exact sequence is one which is exact at every term at which the condition makes sense.

Exactness can be used to unify several concepts in group theory. For example, the assertion that the sequence

$1 \stackrel{i}{\rightarrow} G_1 \stackrel{f}{\rightarrow} G_2 \,$

is exact asserts that f is injective. We see this by noting that the only possible homomorphism i from the trivial group has as image the trivial subgroup of $G 1$ consisting of the identity, and the exactness condition is thus that the kernel of $f$ is equal to this trivial subgroup, which is equivalent to the statement that $f$ is injective.

Similarly, the assertion that the sequence

$G_1 \stackrel{f}{\rightarrow} G_2 \stackrel{j}{\rightarrow} 1\,$

is exact asserts that f is surjective. We see this by noting that the only possible homomorphism j to the trivial group has as kernel the whole of $G 2$ , and the exactness condition is thus that the image of $f$ is equal to this group, which is equivalent to the statement that $f$ is surjective.

Combining these, exactness of

$1 \rightarrow G_1 \stackrel{f}{\rightarrow} G_2 \rightarrow 1\,$

asserts that $f$ is an isomorphism.

A short exact sequence is one of the form

$1 \rightarrow G_1 \stackrel{f_1}{\rightarrow} G_2 \stackrel{f_2}{\rightarrow} G_3 \rightarrow 1 . \,$

It expresses the condition that $G 3$ is the quotient of $G 2$ by a subgroup isomorphic to $G 1$ : this may be expressed as saying that $G 2$ is an extension of $G 3$ by $G 1$ .

Some content on this page may previously have appeared on Citizendium.

Exact sequence

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox