Injective function
From Knowino
In mathematics, an injective function or one-to-one function or injection is a function which has different output values on different input values: f is injective if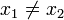 
implies that 
.
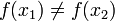An injective function f has a well-defined partial inverse f − 1. If y is an element of the image set of f, then there is at least one input x such that f(x) = y. If f is injective then this x is unique and we can define f − 1(y) to be this unique value. We have f − 1(f(x)) = x for all x in the domain.
A strictly monotonic function is injective, since in this case x1 < x2 implies that f(x1) < f(x2) (if f is increasing) or f(x1) > f(x2) (if f is decreasing).
[edit] See also
|
Some content on this page may previously have appeared on Citizendium. |
