|
יחידה 4: הבינום >> 4.5: קירוב נורמלי של הבינום |
||||
|
קירוב נורמלי של הבינום
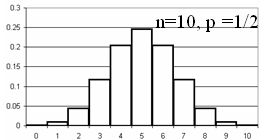
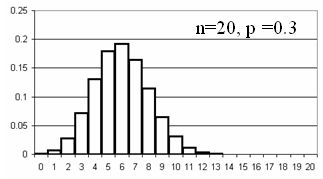
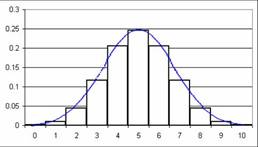
ישנם מקרים בהם צורת ההתפלגות הבינומית מזכירה לנו את צורת ההתפלגות הנורמלית. |
||||
|
|
||||
|
גם כאשר , אם מספיק גדול, חוסר הסימטריה שבין הזנבות יהיה זניח. |
||||
|
|
||||
|
מה זה n מספיק גדול?
זו פונקציה של . ככל ש- שונה יותר מ-1/2 כך דרוש גדול יותר.
כלל אצבע: ישנם כללים שונים בספרות. הכלל שלפיו נעבוד בקורס הוא שאם (כאשר הוא הקטן מבין ו- , ניתן יהיה לבצע את הקירוב הנורמלי של הבינום. זאת אומרת שקיימת עקומה נורמלית שאם "נלביש" אותה על ההתפלגות הבינומית, הפער שבין שתי ההתפלגויות יהיה זניח. |
||||
|
מה יהיו הפרמטרים של העקומה הנורמלית?
ניתן להוכיח ש:
|
||||
|
לדוגמא אם זורקים מטבע 10 פעמים, כמה פעמים אנו נצפה שייפול על עץ? |
||||
|
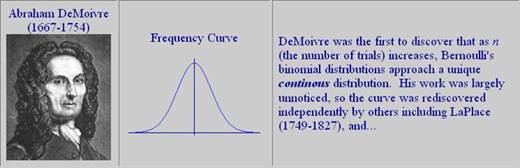
כמו כן ניתן להוכיח ש: . זאת סטיית התקן של התפלגות הדגימה של הבינום ולכן אין לחלק אותה ב- , בניגוד להתפלגות הדגימה של הממוצעים שהכרנו בסמסטר שעבר. זהו פיתוח של De Moivre-Laplace, המבוסס על: . |
||||
|
|
||||
|
|
||||
|
|
||||
|
תיקון לרציפות
ההתפלגות הבינומית היא בדידה ואילו ההתפלגות הנורמלית רציפה. לכן, בקירוב הנורמלי אנו נבצע תיקון לרציפות (שימוש בגבולות אמיתיים). |
||||
|
דוגמא להשוואת קירוב נורמלי של הבינום לבינום רגיל: מתוך 10 זריקות מטבע ב-7 התקבל עץ. האם המטבע הוגן ברמת בטחון של 95%? |
||||
|
|
||||
|
לפי הבינום המדויק: |
||||
|
הסיכוי לקבלת 7 או יותר גדול מ- ולכן לא ניתן לדחות את השערת האפס ברמת בטחון של 95%. |
|
|||
|
עכשיו נבדוק לפי הקירוב הנורמלי: |
||||
|
|
||||
|
|
||||
|
לפי הקירוב הנורמלי: - בדקנו 6.5 כי אנו מעוניינים לבדוק האם 7 נופל בתוך איזור הדחייה. דהיינו אנו מעוניינים לבדוק את הסיכוי לקבל 7 ומעלה ומכיוון שההתפלגות כעט רציפה הגבול האמיתי התחתון של 7 הוא 6.5.
|
||||
|
בזנב התחתון "נוסיף" 1/2 כי נרצה לבדוק את הסיכוי של ערך מסוים ומטה, דהיינו הסיכוי לקבל עד לגבולו העליון האמיתי של מספר מסוים. הכלל הוא תמיד להקטין את Z בערכו המוחלט.
ב-applet הבא ניתן לראות את הקירוב הנורמלי להתפלגות הבינומית. ניתן תחילה לבנות התפלגות דגימה לפי ו- . לאחר מכן ניתן להזין את ההסתברות לקבלת ערך מסוים או ממנו ועד סוף ההתפלגות על ידי הזנת טווח הערכים. כמו כן, ניתן להשוות ב-applet הבא בין התפלגויות דגימה שונות וההתפלגות הנורמלית. |
||||
|
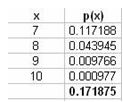
עכשיו נבדוק ב-EXCEL:
או לחלופין עמודת C בטבלת z. כפי שניתן לראות הפער שבין החישוב המדויק (0.1719) לבין החישוב המבוסס על הקירוב הנורמאלי (0.1712) באמת זניח. |
||||
|
דוגמא: ידוע כי בכלל האוכלוסייה ההסתברות להיות חולה בשפעת ביום נתון היא 0.4. המורה שושנה חוששת שמאחר ותלמידיה לא אוכלים מספיק ירקות, המערכת החיסונית שלהם פגיעה יותר ולכן סיכויים לחלות גבוה יותר. ביום מסוים, מתוך 15 תלמידים חלו 12. האם ניתן לומר ברמת בטחון של 95% שמספר החולים גבוה במיוחד? |
||||
|
|
||||
|
פתרון: |
||||
|
, ולכן ניתן לבצע קירוב לנורמלי. |
||||
|
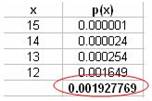
לפי הבינום המדויק: |
|
1. הנחות: אין תלות בין הילדים. |
||
|
|
|
2. השערה: - כי זה מספר החולים שהיינו מצפים עבור 15 ילדים |
||
|
|
|
3. רמת מובהקות: , השערה חד-צדדית |
||
|
|
4. בדיקת ההשערה:
|
|||
|
5. מסקנה: לכן ברמת בטחון של 95% ניתן לדחות את ומספר החולים חריג במיוחד |
||||
|
טעות נפוצה: לחלק את סטיית התקן ב- . אבל אין לעשות זאת מכיוון שכפי שהוסבר לעיל זוהי כבר סטיית תקן של התפלגות הדגימה. |
||||
|
מהי עוצמת המבחן שביצעת אם ידוע שבקרב ילדים שלא אוכלים מספיק ירקות הסיכוי לחלות בשפעת הוא 0.5? |
||||
|
|
||||
|
חישוב אזור הדחייה: |
||||
|
: תחילת אזור הדחייה |
||||
|
אבל חייבים לעבור למספרים בדידים. אם מספר נופל ב"חלקו" באזור הדחייה ו"חלקו" באזור אי הדחייה הוא יהיה כולו באזור אי הדחייה. אם לא היינו שמים אותו באזור אי-הדחייה אז היינו מגדילים את . במקרה שלנו 9 נופל בחלקו באזור אי הדחייה לכן הוא ישתייך לאזור אי הדחייה.
אזור הדחייה: . עוצמת המבחן שווה להסתברות לקבל תחת . ועכשיו צריך לחשב מה הסיכוי לקבל 10 ומעלה כאשר . |
||||
|
שימו לב: בניגוד למבחנים שלמדנו עד כה בהם הנחנו שסטיית התקן של שווה לסטיית התקן של , הרי שבקירוב הנורמלי של הבינום סטיות התקן אינן שוות מכיוון שסטיית התקן מושפעת מה- . |
||||
|
עכשיו מוגדר לנו השטח של העוצמה לפי כפי שהכרנו בהתפלגות Z:
|
||||
|
|
||||