יחידה 9: ציוני תקן וההתפלגות הנורמלית  >> 9.2: ההתפלגות הנורמלית

ההתפלגות הנורמלית

ציון התקן משמש כמדד למיקום יחסי. התפלגות חשובה מאוד בה מחשבים את ציוני התקן היא ההתפלגות הנורמלית.

בהתפלגות הנורמלית ניתן להמיר את ציוני התקן לאחוזונים.

לעובדה זו השלכות חשובות ביותר, ועליה מבוססים מבחנים סטטיסטים רבים.

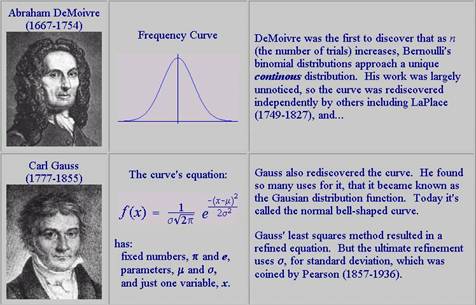
הראשון שחקר את ההתפלגות הנורמלית היה DeMoivre (1667-1754), מטרתו הייתה ניבוי הסתברויות בהימורים.

הראשון שהשתמש בהתפלגות זו במדעי החברה היה , Quetelet (1796-1874), הוא מדד את היקף החזה וגובה של חיילים, ומצא ששניהם מתפלגים נורמלית. הוא הסיק שהממוצע הוא אידיאל הטבע ושסטיות ממנו הן סטיות מאידיאל זה.

 Gauss (1777-1855)עסק (בין היתר) בטעויות מדידה וביסס מודלים על ההתפלגות הנורמלית.

בהתפלגות נורמלית, אם ידועים לנו הממוצע וסטיית התקן נוסחת הקו ידועה, ולכן אפשר לחשב במדויק את השטח תחת העקומה עד לציון מסוים באמצעות חישוב אינטגרל.

שטח זה) יחסית לכלל שטח העקומה( הוא בעצם האחוזון של הציון (במונחים שבין 0 ל-1).

זוהי נוסחת העקומה הנורמלית:

ע"מ שלא נצטרך לחשב אינטגרלים, סטטיסטיקאים חישבו את האחוזונים של מספר רב של ערכים, בציוני תקן. כך שאם נמיר את הערך הגולמי הרצוי לציון תקן, נוכל לבדוק בטבלה את האחוזון של הציון המבוקש. ניתן לעשות זאת משום שהמרה לציוני תקן הינה טרנספורמציה לינארית אשר לא משפיעה על היחסים שבין מרווחי המספרים.

ניתן, כמובן, במקום להשתמש בטבלה, להיעזר ב-EXCEL – הפקודה ב-EXCEL הינה NORMSDIST ונדגים אותה בהמשך.

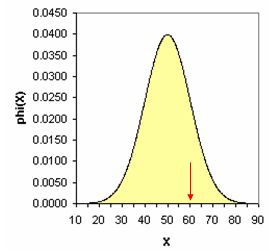
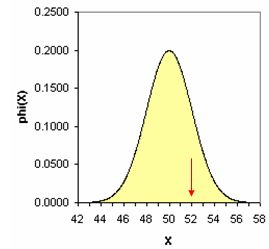
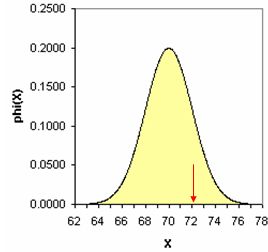
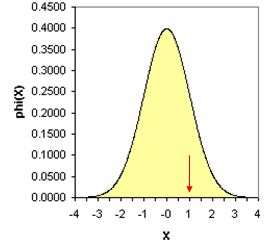
בגרפים שלהלן מוצגות התפלגויות שונות עם ממוצעים שונים וסטיות תקן שונות.

החץ המצביע על הערך נמצא באותו מרחק (סטיות תקן) מהממוצע אך הערך הגולמי שונה. העקומה האחרונה הינה בציוני תקן. בכדי שנוכל להשוות בין עקומות שונות יש להמיר את הציונים לציוני תקן. מכיוון שכאן ההתפלגויות הן התפלגויות נורמליות ניתן אף לחשב את אחוז המקרים בין הערך לממוצע, מעבר לערך וכו'.

תִקנון כלל ההתפלגויות שלעיל מביא להתפלגות נורמלית סטנדרטית:

שימו לב: אם ההתפלגות המקורית היא נורמלית, תקנון הערכים יניב התפלגות נורמלית סטנדרטית.

אם ההתפלגות המקורית אינה נורמלית, תקנון הערכים יניב התפלגות סטנדרטית.

► חזור                    המשך ◄