5. POLAROGRAPHY

5.1. Polarographic methods

In direct current polarography (DCP) a constant potential is applied during the entire drop-life time. A current-voltage curve is constructed by applying a series of potential steps, each step being synchronized with the drop fall. In most instruments, however, linearly changing potential is applied, with a rate slow enough that the change of potential throughout the drop-life time is about a few millivolts. The current is measured at the end of the drop life.

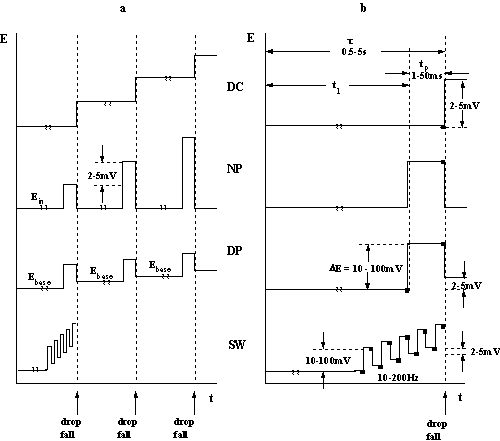
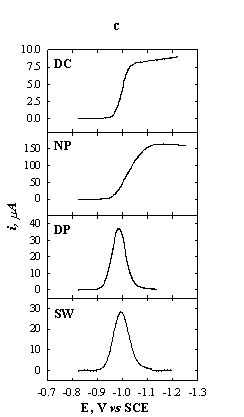
Fig.5-1 Schematic presentation of some polarographic methods.

(a) Potential sequence of a polarogram.

(b) Potential sequence on a single drop (n current sampling).

(c) Current-potential curves for 1 mM Zn²⁺ in 1 M KNO₃.

DC: t = 2 s; NP: t = 2 s, t_p = 5 ms; DP: t = 2 s, t_p = 5 ms; DE_p = 20 mV;

SW: delay time = 4 s, DE_p = 20 mV, f = 100 Hz.

In normal pulse polarography (NPP) the mercury-drop electrode is held for most of its duration at a constant potential E_in, at which no electrochemical reaction takes place under given experimental conditions. The potential of interest E_p is applied in the last stage of the drop life, for a length of time t_p (of the order of few milliseconds). The values of E_in and t_p are kept constant throughout the recording of the polarogram and E_p is changed from drop to drop (Fig.5-1a).

The limiting current in NPP is diffusion controlled. The experimental requirements for diffusion control are the same as those for DC polarography. Since t_p is of the order of milliseconds, the diffusion layer thickness is very small compared to the radius of the mercury drop reached at the end of its life. The equations for planar diffusion can be applied with much better agreement than for DC polarography (for t_p = 1 ms, the diffusion layer thickness is about 2·10^-4 cm, while the radius of the mercury drop is about 0.05 cm at t = 5 sec and m = 1 mg/sec). Furthermore, the area of the drop is virtually constant during the application of the pulse (t is much larger than t_p). The constancy of the area implies also that no correction factor for the expansion of the diffusion layer is required (the (7/3)^1/2 factor). Thus,

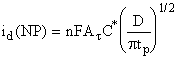(1)

For comparison, the current for DC polarography at time t is

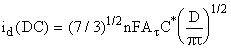(2)

The current under NP conditions is larger than that under DC conditions. The enhancement of the current is

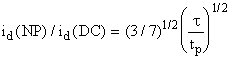(3)

For typical conditions, t = 5 s and t_p = 5 ms, this ratio is about 20. The contribution of the charging current is identical for both NPP and DCP, and thus the detection limit of NPP is lower than that of DCP by an order of magnitude.

The i/E relationship for Nernstian processes at DCP and NPP is given by

(4)

The detection limit of NPP is about 2·10^-7 M.

Differential pulse polarography (DPP). From analytical point of view, the sensitivity of DPP is even better than that of NPP. The potential sequence on a single mercury drop and the potential sequence used for recording an entire differential pulse polarogram are given in Fig.5-1. The current is sampled twice during a drop life-time: (i) at t₁, just before the pulse, and (ii) at t, just before the drop fall. The polarogram represents the current difference as function of the base potential E_b. The curve is peaked shaped. The height of the peak is proportional to the concentration of the electroactive species.

For Nernstian processes Ox + ne = Red and C*_red = 0, the faradaic component of the current at the peak and E_peak are

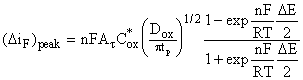(5)

(6)

The peak form of the DP voltammogram is explained below. At sufficiently positive potentials, E_b - E⁰ > (120/n) mV, the faradaic currents and i(t₁) are both zero, and thus also is zero. At sufficiently negative base potentials, E_b - E⁰ < (120/n) mV, the faradaic process proceeds at maximum rate and the diffusion-limited current is reached; the current is independent of potential and s zero. At potentials in the vicinity of the current difference is determined by and has a finite value.

For non-Nernstian processes is smaller than for Nernstian ones. The sensitivity and the detection limit of DPP are better for Nernstian processes, while for DC and NP polarography, they are independent of the type of the processes. The reason for this can be understood by noting that the equations for the limiting current in DC and NP polarography (eqs.1 and 2) do not contain assumptions about Nernstian processes. For the case of DPP, however, the value of is derived from the variation of the current around The derivative di/dE for non-Nernstian processes is smaller than for Nernstian, and results in a lower peak.

Although (Di_F)_peak is smaller than the limiting current at NPP, the detection limit at DPP is lower (about 10^-7 M) due to the efficient compensation for the charging current.

Square wave polarography (SWP). High sensitivity and low detection limit are obtained with this technique. It is similar to DPP, however, the entire potential sequence is applied during the life-time of a single drop. The voltammogram is obtained in a few seconds, compared to much longer times with the other techniques.

The potential sequence is applied several seconds after the drop birth, in order to take advantage of a larger surface area of the mercury drop.

As in the case of DPP, the difference of the current before and after the application of the pulse is measured. The performance of the method is better for Nernstian processes than for non-Nernstian ones. Detection limit of the method is about 10^-7 M.

5.2. Handling the dropping-mercury electrode (DME)

The mercury capillary may be easily clogged and care must be exercised to prevent contamination. The DME must never be allowed to stand in solution when mercury is not flowing. Before allowing any solution to come in contact with the DME, raise the leveling bulb and check that mercury drops are formed at the end of the capillary. Allow the mercury flow during the entire laboratory session. After use, the capillary should be washed thoroughly with distilled water. The mercury reservoir is then lowered to stop the flow.

Note: BE AWARE! Mercury vapors are poisonous!

Notify the instructor in the event of mercury spill. Mercury should be cleaned up immediately. Do not throw it down the drain.

Reference electrode

An Ag/AgCl/1 M KCl reference electrode is used. Its potential is -19 mV vs SCE.

Chemicals 1. 1 M KNO₃

2. 0.1 M KNO₃

3. 5.00 mM ZnCl₂

4. 0.2 % Triton X-100

5. 0.01 M TlNO₃

6. 0.01 M KIO₃

7. 0.1 M NaCl

8. 0.1 mM Tl⁺, 0.1 mM Cd²⁺, 0.1 mM Zn²⁺, 0.1 mM Ni²⁺, 0.002 % Triton X-100

in 0.1 M NH₄OH - 0.1 M NH₄Cl buffer

9. 0.5 M acetate buffer (pH 4.6)

10. 0.2 % ascorbic acid (freshly prepared)

Exp. 1. Oxygen waves

Fill the polarographic cell with 0.1 M KNO₃ without passing the deaeration step. (Ask the instructor for help). Record the polarogram using a voltage range of 0.2 to –1.8 V and a suitable current sensitivity (, t_p = 20 ms, pulse amplitude = 20 mV, scan rate = 10 mV/s). Mark on the polarogram, what are the electrode processes that take place at each wave. Estimate the concentration of dissolved oxygen, assuming that the mercury flow rate is 1 mg/sec and D = 2·10^-5 cm²/s.

After the first polarogram has been obtained, empty the cell, rinse and fill it with a deoxygenated solution of 0.1 M KNO₃. Run a polarogram of the deaerated solution.

Hereafter, all solutions for analysis should be deaerated.

Exp. 2. Polarographic spectrum

Introduce into the polarographic cell the deoxygenated solution containing 0.1 mM of Tl⁺, Cd²⁺, Ni²⁺ and Zn²⁺. Record the polarogram in the potential range from -0.2 to -1.6 V, using several polarographic modes: DC, NP, DP and SW. Compare E_1/2 values with those found in the literature.

Exp. 3. Capacitance currents

The purposes of the experiments are:

(a) to observe the potential of zero charge, E_Z, at a dropping-mercury electrode by recording i vs E curves in solutions containing supporting electrolyte only;

(b) to measure currents due to charging of the double layer.

Record a polarogram of a deaerated 0.1 M KNO₃ solution at potentials ±200 mV around E_Z (E_Z = -0.45 V vs SCE, in absence of specific adsorption). Use an expanded potential scale.

Record a current-time plot for a single drop at E = E_Z. Repeat for a potential positive and a potential negative to E_Z. Do not forget to mark the zero current. Determine the value of E_Z and compare with data in literature.

Analyze the current/time plots and compare with theory. Estimate from the current/time plots the double layer capacitance, assuming m = 1 mg/sec.

Exp. 4. Maxima and maxima suppression

Run a polarogram of 1 mM Zn²⁺ in 0.1 M NaCl. Repeat the experiment with the same solution, containing 0.002% Triton X-100. Note the effect of the detergent on both the peak and the limiting current.

Exp. 5. Migration currents

The purpose of the experiment is to test the effect of the concentration of the supporting electrolyte on the limiting current. For this purpose run polarograms of 1 mM Tl⁺ solution with increasing concentrations of KNO₃ (0, 1, 2, 5, 10, 50, 100 mM). Use the potential range of –0.1 to 1.0 V (, t_p = 20 ms, pulse amplitude = 20 mV, scan rate = 10 mV/s). Plot the limiting current vs concentration of supporting electrolyte. Compare with theory, assuming equal equivalent conductances for all ionic species of interest.

Repeat the experiment by replacing the Tl⁺ solution with KIO_3. In that case 0.002% Triton X-100 is required to suppress the polarographic maxima. Use the potential range of –0.8 to -1.8 V. The electrode reaction of the reduction of KIO₃ is:

Exp. 6. Analysis of the polarographic wave

The purposes of the experiment are:

(a) to verify that the limiting current of the TI⁺ - reduction polarographic wave is diffusion controlled;

(b) to determine the half-wave potential and the number of electrons involved in the reduction.

Prepare 0.5 mM solution of TlNO₃ in 0.1 M KNO₃. (The Tl⁺ concentration has been chosen low enough in order to neglect potential drop in the solution). Run a polarogram in order to choose a potential in the limiting current region. Record a current/time plot at the chosen potential. Prove, that the current is totally diffusion controlled, and calculate the diffusion coefficient, assuming that m = 1 mg/sec.

In order to enable an accurate measurement of the currents along the wave, run an additional polarogram at a slow scan rate (5 mV/s).

Determine E_1/2 of the Tl⁺ reduction wave and compare with literature.

Determine the number of electrons involved in the reduction process from E vs log[(i_d -i)/i] plot.

Exp. 7. Quantitative determination of Zn²⁺ in drinking water

Fill the cell with the sample of drinking water and record a polarogram. You may prefer to use one of the more sensitive polarographic methods (normal pulse, differential pulse or square wave). Make a rough estimation of the concentration of Zn²⁺.

For the analytical determination use both the standard addition method and the calibration curve method. Show the instructor your detailed plan of operation, including the composition of the solutions. Prepare the standard solutions in 50 ml volumetric flasks. For the calibration curve method use as the supporting electrolyte the solution of 10 mM NaCl. Compare the results of the two methods of determination.

Exp. 8. Determination of ascorbic acid (Vitamin C) in citrus juice by the standard-addition method.

Ascorbic acid yields a well-defined polarographic oxidation wave. The determination can be carried out directly in freshly prepared diluted juice as well as in conserved citrus juice. The method of standard additions is used for the quantitative determination of the concentration of the Vitamin C.

Ascorbic acid	Dehydroascorbic acid

Procedure

1. Calibration curve

Prepare a fresh stock solution of 50 ml 0.2 % ascorbic acid.

Prepare five standard solutions of ascorbic acid in volumetric flasks of 25 ml. To each one add 0.5 ml 0.5 M acetate buffer and different volumes of 0.2 % ascorbic acid: 0, 200, 400, 600 and 800 . Dilute to the mark with distilled water.

For each solution record a NP (, t_p = 20 ms, pulse amplitude = 20 mV, scan rate = 10 mV/s) and SW (, t_p = 20 ms, pulse amplitude = 20 mV, scan rate = 100 mV/s) polarograms over the potential range: -150 to +200 mV vs. Ag/AgCl/1 M KCl, with E_in = -150 mV. Consult with the instructor about the preferable mode of polarography to be used in further experiments.

Plot i_d vs. concentration of ascorbic acid. Is the plot linear and does it pass through the origin? On the basis of these observations decide if the standard-addition method is applicable.

2. Determination of ascorbic acid in citrus fruits

Squeeze an orange, grapefruit or lemon until about 10 ml of juice is obtained. Filter the juice through a porous funnel (pore size about 1 mm).

Prepare four 25 ml volumetric flasks. Add to each, 0.5 ml of 0.5 M acetate buffer, 2.0 ml of the juice and standard additions of 0, 200, 400 and 600 of 0.2 % ascorbic acid. Dilute to the mark with distilled water.

Record polarograms under the same conditions as in the calibration step.

Draw the standard additions plot and determine the concentration of the analyte. Report the concentration of ascorbic acid (Vitamin C) in the original sample (juice) in mol/l and ppm.

3. Determination of ascorbic acid in conserved citrus juice

Plan an experiment for the determination of ascorbic acid in preserved (commercial) citrus juice. Use the scheme of the previous experiment. Consult with the instructor as to the differences in procedure for preserved as opposed to natural juice.

Recommended Literature

1. H. H. Willard, L. L. Merritt, J. A. Dean and F. A. Settle, Instrumental Methods of Analysis.

2. D. A. Skoog and D. M. West, Principles of Instrumental Analysis.

3. D. A. Skoog and J. J. Leary, Instrumental Analysis.

4. D. C. Harris, Quantitative Chemical Analysis.

5. A. J. Bard and L. R. Faulkner, Electroanalytical Chemistry.

Go to Main Page