Symbolic Logic:Programming:Value Set
A Value Set is a type which is used to record a set of values allowed for a variable, attached to possible worlds. Value Sets allow us to reason about variables that may take multiple values.
A Value Set is a set of possible values for a variable. Evaluation proceeds by "narrowing" this collection of values until only solution values are left. We need to know which "situation" each value is derived from. These situations are called possible worlds.
To describe Value Sets we first introduce possible worlds and then describe value sets in terms of possible worlds. Then we describe rules for working with Value Sets.
Contents |
[edit] Introduction
Sometimes a variable may have multiple values,
Also the logic operations that allow multiple values.
If we have functions, they should return one value. Then everything is nice and we can feed that value into the next function and get out results without having to think.
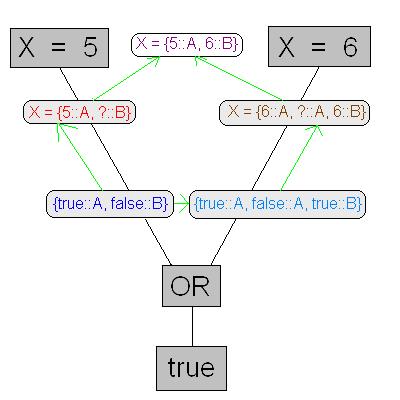
What if we could write,
meaning that the set {2, -2} is the result set. Naively we could calculate results by applying functions to all combination's of the values. However there are problems,
Naively the resulting values are 2+2, 2+-2, -2+2, -2+-2. So 3 values are possible, -4, 0, 4.
But clearly x+x does not equal 4. To get around this problem we need to tag the values with the where the value come from.
Suppose you toss a coin. The result is ether heads or tails. The result cant be both. Its one or the other. These are two different future situations.
So what do we call these future situations? In fact they may not even be in the future. I call them Possible Worlds.
The behaviour of Value Sets is worked out below. Value Sets allow us to work with logic in an easy an intuitive way. And they allow the computer to do the same.
Languages like Prolog handle logic by trying out possibilities and back tracking when they prove inconsistent. Using Value Sets that is not necessary. All calculation is then the evaluation of functions, similar to (but not the same as) Functional Programming].
[edit] How it works
In our example above,
insert picture here,
The result is,
Then
But 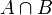 is impossible. It is like the coin turning up heads and tails at the same time. So,
is impossible. It is like the coin turning up heads and tails at the same time. So,
Using some simple rules the same method may be applied to any situation.
[edit] Possible Worlds
In general a Possible World may be thought of as an alternate possible reality that may eventuate under certain conditions.
Specifically in our case a Possible World is described by facts about the values of variables. The possible world is regarded as a set of outcomes and is represented in set builder notation like,
Note that we dont actually specify what the elements of the set are. The elements could be regarded as tuples of values of variables, but this is not necessary for our purposes.
In implementing a Constraint Logic Programming system Possible Worlds are not used to record boolean conditions. Possible Worlds are represented by their identity, and there hierarchical relationship.
However in proving theorems we will regard Possible Worlds as sets controlled by boolean conditions.
[edit] Possible World Set
A Possible World Set is a Partition of a Possible World P. It is a set of possible worlds S such that,
- if
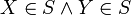 then
then 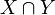 is empty.
is empty.
[edit] Value Set
A Value Set has a set of tagged values. Each value is "tagged" with a possible world that allows us to track the value against a possible world in a calculation. A tagged value is defined by the operator ::
this is purely a notation. The above is a tuple and could also have been written,
The value of 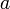 is
is 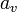 .
The possible world of
.
The possible world of 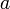 is
is 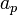
There are multiple ways of representing the same value set. All the representations are regarded as equivalent. Two Value Sets are equal if they represent the same set of values.
Value Sets are used to model the set of solutions to equations,
[edit] (A) Definition of a Value Set
A Value Set is intended to represent the possible values for a variable, attached to possible worlds. For each expression 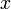 there is a Value Set
there is a Value Set 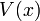 .
.
[edit] Notation
A Value Set has a Tagged Set. The distinction is kept because two Value Sets are regarded as equal when there Tagged Sets are not.
- The Tagged Set of the Value Set
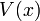 is written
is written 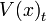 .
.
- The Value Set constructed from a tagged set
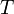 by
by 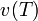
If 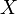 is a value set, its set of expression values is
is a value set, its set of expression values is 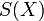 where,
where,
The set of possible worlds is W(X) where,
[edit] Definition A1
Description
- A variables value is in the value set of expression values from non empty possible worlds.
Definition
[edit] Definition A2
Description
- Two Value Sets are equivalent if their expression sets are identical.
Definition
[edit] Definition A3
Description
- A World Set covers all possiblities.
Definition
[edit] Definition A4
Description
- The possible world for a value for a variable, must have that variable with that value.
Definition
[edit] Definition A5
Description
- Asserting a value set is equivalent to asserting the value.
Definition
This is the definition of what it means to type cast a value set to boolean. If a variable is of type boolean then its value set, type cast to boolean, is equal to the value.
[edit] Definition A6
Description
- The value set of a function call on a variable is the same as the value set of the function set applied to the value set of the variable.
Definition
for constant functions this reduces to,
[edit] Basic Theorems
[edit] Theorem T1
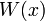 is a partition of
is a partition of 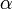 .
.
This follows from A3 and A4.
[edit] Theorem T2
[edit] (B) Functions of a Value Set
The following theorem gives the function on a value set of a type using the function of the type.
- (B1)
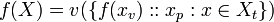
[edit] Function of Multiple Parameters
If we allow Currying then we can extend the above definition to multiple parameters.
If currying is allowed,
The following theorem may then be used,
If F is a value set of functions on a value set of a values,
- (B2)
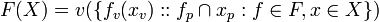
[edit] Function of two parameters
Then the definition for value sets of functions may be applied giving,
or,
- (B3)
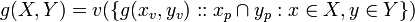
The result can be extended to more parameters.
[edit] Function of Vector of Parameters
The result may be generalised to multiple parameters. If x is a vector, and X is a vector of Value Sets (representing multiple parameters) then,
- (B4)
![F(X) = v(\{ f(x_v)::\bigcap_{j \in J} x_p[j] : x\in X \}) \!](../w/images/math/a/e/1/ae1c62730114fb145296aef6ff5f018f.png)
[edit] (C) Assertions on Value Sets
The above rules allow us to transform a function of variable values into a function about value sets. A statement is a function that is asserted to return the true boolean value. A statement may be transformed into a function that returns a value set.
This is unusual because we dont normally assert a set to be true. But we can think of this polymorphically. A statement returning a value set may be treated differently from a statement returning a boolean.
In this case if V is a value set, the following law applies,
- (C1)
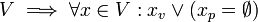
In words, if we assert a Value Set then for every tagged value in the set either the value is true or its possible world is empty. A value tagged with an empty possible world is an impossible value,
- (C2)
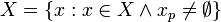
In other words you can remove all values tagged with the empty possible world from a value set.
[edit] (D) Resolution
If two Value Sets are equated all but the matching values are removed. This implies that some the Value Sets that dont match are empty. This may mean that other Possible Worlds that are also empty. How do we determine when this occurs?
Definition:
- If X is a child of Y, and no Possible World in X is a member of a Possible World in Y then it is empty, as long as the Possible Worlds are in the standard form.
This rule is important in resolving the effects of pruning of Value Sets on each other.
The standard form for Possible Worlds is defined as,
The formulas for functions of Value Sets are in this form. The form is only broken if Possible Worlds with the same value are merged. This is the form that will be used in the CLP implementation.
If 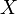 ,
, 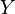 and
and 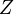 are a Value Sets, where
are a Value Sets, where
then,
[edit] Examples
[edit] Example 1
Clearly x = 2. But I want to show how this value is derived using value sets. Ultimately the application of these rules is automated into a logic programming system.
[edit] Step 1: Apply A
Using T2,
Using A5 and A6,
[edit] Step 2: Apply B
Using (B1) on 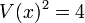 ,
,
which simplifies down to,
[edit] Step 3: Apply C
Using (C1),
gives 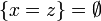 unless
unless 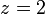 or
or 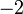 ,
,
Using (C2) on 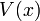 tagged values from empty possible worlds can be removed without changing the value of the Value Set.
tagged values from empty possible worlds can be removed without changing the value of the Value Set.
[edit] Step 4: Apply B again
Using (B1) on 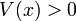 ,
,
[edit] Step 5: Apply C again
Using (C1) on V(x > 0),
gives 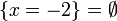 and so,
and so,
So using (C2) on 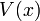 drop the tagged value with
drop the tagged value with 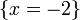 .
.
then from (A1),
[edit] Example 2
This example shows how repeated use of a variables are handled. Naively,
But this possiblity is removed because the two values are from possible worlds whose intersection is empty.
[edit] Step 1: Apply A
Applying (A1a),
And using A6,
[edit] Step 2: Apply B
Using (B3),
but,
this is obvious in the example but the law used is that the two possible worlds are from the same World Set,
or using C3,
[edit] Step 3: Apply A
[edit] Implementation
Constraint Logic Programming systems implements the logic of Value Sets. As part of this implementation the relationship between Value Sets and Possible Worlds is modelled.
[edit] Modelling Possible Worlds and Possible World Sets
Full details of the Possible Worlds do not need to be modelled. The Constraint Logic Programming System only needs to know if the Possible World is empty or not.
The rules in Functions Of a value set describe how values are combined,
- (B3)
![F(X) = v(\{ f(x_v)::\bigcap_{j \in J} x_p[j] : x\in X \}) \!](../w/images/math/a/e/1/ae1c62730114fb145296aef6ff5f018f.png)
The Possible World is then,
If any of the component ![x_p[j] \!](../w/images/math/0/7/d/07db62b455c4edfbd7d869001c332c16.png) are empty then
are empty then 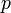 is empty.
is empty.
If none of the ![x_p[j] \!](../w/images/math/0/7/d/07db62b455c4edfbd7d869001c332c16.png) are empty, the product will still be empty if more than one of the
are empty, the product will still be empty if more than one of the ![x_p[j] \!](../w/images/math/0/7/d/07db62b455c4edfbd7d869001c332c16.png) are from different values in the same Value Set. As the Possible World Set is a partition the intersection must be empty in that case.
are from different values in the same Value Set. As the Possible World Set is a partition the intersection must be empty in that case.
[edit] Links
- Symbolic Logic:Programming:Value Set Implementation
- Symbolic Logic:Programming:Value Set Programming
- Symbolic Logic:Programming
- Intelligence and Reasoning

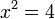
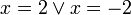
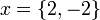
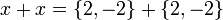
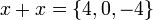
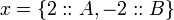
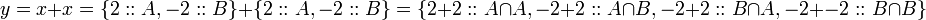
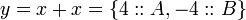
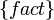
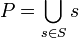
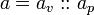
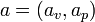
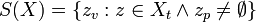
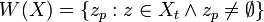
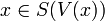
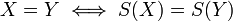
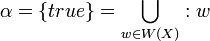
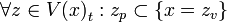
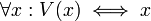
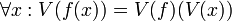
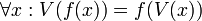
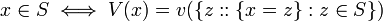
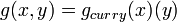
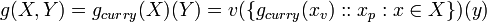
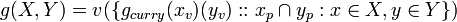
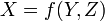
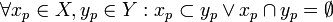
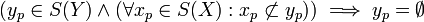
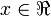
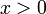
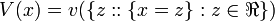
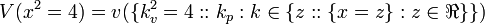
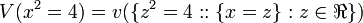
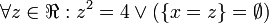
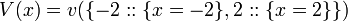
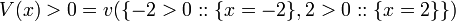
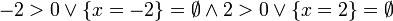
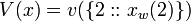
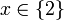
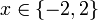
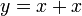
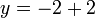
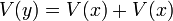
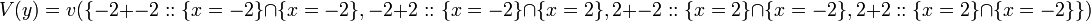
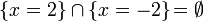
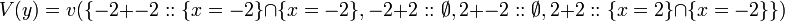
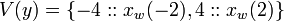
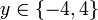
![p = \bigcap_{j \in J} x_p[j] \!](../w/images/math/0/0/3/003a77ee80dfed12e234802963be193e.png)