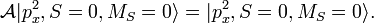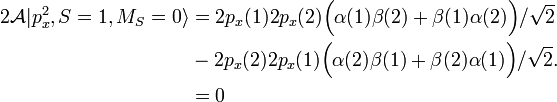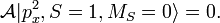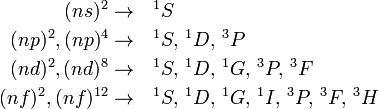Russell-Saunders coupling
In atomic spectroscopy, Russell–Saunders coupling, also known as LS coupling, specifies a coupling scheme of electronic spin- and orbital-angular momenta. The coupling scheme is named after H. N. Russell and F. A. Saunders (1925).[1] Russell-Saunders coupling is useful mainly for the lighter atoms, roughly for atoms with atomic number less than 57. For heavier atoms j-j coupling gives a better approximation for atomic wave function.
Contents |
[edit] Description
Consider an atom with n electrons. In Russell-Saunders coupling the orbital angular momentum eigenstates of these electrons are coupled to eigenstates with quantum number L of the total angular momentum operator squared L2, where the angular momentum operator is,
Separately the one-electron spin functions are coupled to eigenstates with quantum number S of total spin angular momentum squared S2. Sometimes there is further coupling to J ≡ L + S. The resulting L-S eigenstates are characterized by term symbols.
Consider, as an example, the excited helium atom in the atomic electron configuration 2p3p. By the triangular conditions the one-electron spins s = ½ can couple to |½−½|, ½+½ = 0, 1 (spin singlet and triplet) and the two orbital angular momenta l = 1 can couple to L = |1−1|, 1, 1+1 = 0, 1, 2. In total, Russell-Saunders coupling gives two-electron states labeled by the term symbols:
- 1S, 1P, 1D, 3S, 3P, 3D,
The dimension is 1×(1+3+5) + 3×(1+3+5) = 36. The electronic configuration 2p3p stands for 6×6 = 36 orbital products, as each of the three p-orbitals has two spin functions, so that in total there are 6 spinorbitals with principal quantum number n = 2 and also 6 spinorbitals with n = 3. A check on dimensions before and after coupling is useful because it is easy to overlook coupled states.
Russell-Saunders coupling gives useful first-order states in the case that one-electron spin-orbit coupling is much less important than the Coulomb interactions between the electrons and can be neglected. This occurs for the low Z part (i.e., the lighter elements) of the periodic table, roughly up to the lanthanoids (previously lanthanides, starting at Z = 57) . The usefulness stems from the fact that states of different L and S do not mix under the total Coulomb interaction, so that LS coupling achieves a considerable block diagonalization of the matrix of a Hamiltonian in which spin-orbit coupling is absent.
In the high Z regions of the periodic system it is common to first couple the one-electron momenta j ≡ l + s and then the one-electron j-eigenstates to total J. This so-called j-j coupling scheme gives a more useful first-order approximation when spin-orbit interaction is larger than the Coulomb interaction and spin-orbit interaction is included, while the Coulomb interaction is neglected. If, however, in either coupling scheme all resulting states are accounted for, i.e., the same subspace of Hilbert (function) space is obtained, then the choice of coupling scheme is irrelevant in calculations where both interactions—electrostatic and spin-orbit—are included on equal footing.
[edit] More complicated electron configurations
[edit] Spin coupling
Let us consider how to couple n spin-½ particles (electrons) to eigenstates of total S2.
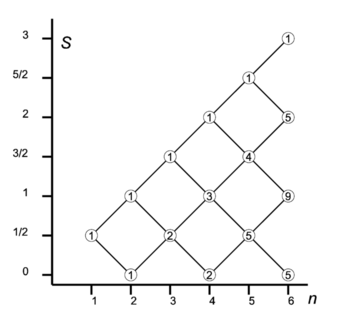
The one-electron system (n = 1) has two functions with s = ½ and m = ± ½ (spin up and down). It was shown that addition of an electron leads to four two-electron spin functions: a singlet (2S + 1 = 1) and a triplet space (a "ladder" of 2S + 1 = 3 spin functions). If one adds one spin to the two-electron triplet (S = 1), the triangular conditions tell us that S = 3/2, and S = 1/2 can be obtained. In the diagram on the right we see that two lines depart from the n = 2, S = 1 node. One line goes up and joins the n = 3, S = 3/2 node, the other goes down and joins the n = 3, S = 1/2 node.
A two-particle spin system also has a spin-singlet S = 0. Adding a spin to it leads to a doublet, S = 1/2. It can be shown that the doublet thus obtained is orthogonal to the doublet with the intermediate (n = 2, S = 1) spin triplet. Two different paths lead two different—even orthogonal—three-electron spin doublets. This is why the number 2 is listed in the circle at the n = 3, S = 1/2 node.
From the two doublets it is possible, by again adding one electron, to create two four-electron singlets, and two four-electron triplet spaces (ladders). A four-electron triplet space can also be obtained from the three-electron quadruplet (S = 3/2) by subtracting S = 1/2. Hence the number 3 is found at the n = 4, S = 1 node. It is the sum of numbers in the nodes directly on its left connected to it.
The system of sequentially coupling one electron at the time should be clear now. Every path in the branching diagram corresponds to a unique (2S+1)-dimensional ladder of eigenfunctions of total spin angular momentum operator S2 with spin quantum number S. Ladders belonging to different paths are orthogonal. The number in the circle indicates how many paths have this node as endpoint.
It is of interest to check dimensions. For instance, the total spin space of five electrons is of dimension 25 = 32. Reading from bottom to top in the diagram, one finds 5×2 + 4×4 + 1×6 (second factors being 2S+1), which indeed adds up to 32.
The actual coupling of electron n to a state of n − 1 electrons uses special values of Clebsch-Gordan coefficients. Let us use k as a path index (e.g., for S = 1 and n = 6, the index k runs from 1 to 9). Then addition (line upwards) gives the n-electron spin state:
Subtraction (line downwards) gives the n-electron spin state:
In particular, for n = 2 the spin triplet results:
which gives the triplet "ladder", where in the notation the index k = 1 is suppressed,
Here the more common notation for one-electron spin functions (α for m = ½ and β for m = −½) is introduced. Note that all three triplet spin functions are symmetric under interchange of the two electrons.
The two-electron spin singlet follows from (suppressing the path index k = 1 again):
a function that is antisymmetric (changes sign) under permutation of electron 1 and 2.
[edit] Orbital coupling
The one-electron orbital angular momenta l can also be coupled sequentially, i.e., one after the other. Different paths give orthogonal states. Consider as an example the configuration p3. Repeated application of the triangular conditions gives that 33 = 27 dimensional space decomposes as follows in eigenspaces of L2, [with L ≡ l(1) + l(2)+ l(3) ]:
- (2)F, (2)D, (1)D, (2)P, (1)P, (0)P, (1)S
where the two-electron quantum numbers L12 of electron 1 and 2 precede in brackets the letters designating the three-electron angular momentum quantum number. Dimensions are: 7 + 5 + 5 + 3 + 3 + 3 + 1 = 27. There are two orthogonal D spaces and three orthogonal P spaces, while there is only one F and S space (of dimension 7 and 1, respectively).
The algorithm should be clear now. For instance, to decompose the 135-dimensional space belonging to the configuration p3d, one can use the result for p3 and add d to any of the eigenspaces and use the triangular conditions again, as in F × d gives L = 5, 4, 3, 2, 1.
[edit] Equivalent electrons
So far it was ignored the Pauli principle that states that many-electron wave functions must be antisymmetric under simultaneous transposition of spatial and spin coordinates of any pair of electrons. This principle affects considerably the results for configurations of equivalent electrons, which by definition are electrons with the same n (principal) and l (azimuthal or angular momentum) quantum numbers. It will be shown that certain terms (LS states) arising from equivalent electrons are forbidden by the Pauli principle. Terms arising from non-equivalent electrons are never forbidden, they simply give rise to non-vanishing antisymmetric states.
[edit] Two-electron atoms
Let us take as an example the spatial product, describing two equivalent electrons, 2px(1)2px(2). Transposition P(12) of space coordinates gives in general:
Hence,
and it follows that the product is symmetric under transposition.
So, there are two-electron singlet and triplet spin functions. In both cases MS = 0 functions are considered, thus,
Antisymmetric functions, satisfying the Pauli principle, are obtained by use of the antisymmetrizer ![\scriptstyle \mathcal{A} = [ (1) - (12) ]/2](../w/images/math/4/c/8/4c885922fbf58fc65ed32b54eca39c36.png) , where (12) transposes simultaneous space and spin coordinates of electron 1 and 2 and (1) is the identity operator (does nothing).
, where (12) transposes simultaneous space and spin coordinates of electron 1 and 2 and (1) is the identity operator (does nothing).
Hence
It follows that the symmetric spatial function 2px(1)2px(2) multiplied by the antisymmetric spin singlet function is an eigenfunction of the antisymmetrizer, that is, the symmetric space times antisymmetric spin function satisfies the Pauli principle.
The calculation for the spin triplet is repeated:
Hence
The symmetric spatial function 2px(1)2px(2) multiplied by the symmetric spin triplet function does not have a non-vanishing antisymmetric component, that is, this space-spin product is forbidden by the Pauli principle.
So, this example shows clearly two important results valid for two particles:
- Spin eigenfunctions of S2 are either symmetric or antisymmetric under transposition of spin coordinates.
- The symmetric orbital function multiplied by a symmetric spin function is Pauli forbidden, i.e., vanishes upon antisymmetrization. The same function multiplied by an antisymmetric spin function is antisymmetric under simultaneous transpositions of space and spin coordinates, and hence is Pauli allowed.
Conversely, it can be shown that an antisymmetric orbital function, for instance: px(1) py(2) - px(2)py(1), can only combine with a symmetric spin function to a non-vanishing—Pauli allowed—totally antisymmetric spin-orbit function.
In general one can show from the symmetry of the Clebsch-Gordan coefficients that eigenstates of L2 for two equivalent electrons with odd quantum number L are antisymmetric under transposition of the electron coordinates. Hence these odd L states must be multiplied by symmetric spin functions (triplets S = 1). In total L+S must be even. The even L states (still for two equivalent electrons) are even under transposition and must be multiplied by odd spin functions (singlets, S = 0). Again L+S must be even in order to get a non-vanishing result upon antisymmetrization.
Before continuing, it must be pointed out that there exists an interesting symmetry between holes and particles. If an electron from a closed subshell is removed a hole is prepared in the subshell. It can be shown that a hole shares many properties with an electron: it has the same orbital and spin angular momentum quantum number. A number of holes must satisfy the Pauli principle in the very same way as an equal number of electrons.
The rule is: L + S must be even for two equivalent electrons. This rule also holds for two equivalent holes. Thus, for instance the carbon atom ground state has two equivalent electrons: 1s22s22p2, which gives 3P, 1D and 1S. The oxygen atom ground state has two equivalent holes: 1s22s22p4, which also gives 3P, 1D and 1S.
Knowing all this one can construct the following table
[edit] Many-electron atoms
When considering more than two electrons, one can ignore closed (sub)shells in the Russell-Saunders coupling because they have L = S = 0.
For more than two electrons (or holes) the theory based on the symmetric group can be extended.[2][3] It can be shown that an N-electron spin eigenfunction of S2 belongs to an irreducible representation of the symmetric group (also known as permutation group) SN. In other words, the concept of symmetry under transpositions can be generalized to more than two particles. This generalized permutation symmetry is enforced on the spin functions by requiring them to be eigenfunctions of S2, a Casimir operator of the group SU(2). The irreducible representations of SU(2) and SN carried by tensor space are intertwined. The antisymmetrizer acting on an orbital product times an eigenfunction of S2 enforces permutational symmetry on the orbital product (carries, so to speak, the permutation symmetry of the spin part over to the orbital part). The permutational symmetry of the orbital product, finally, implies that the orbital product is adapted to the unitary group U(2ℓ+1). The irreducible representations of the latter group carry different eigenstates of L2, that, by construction, are Pauli allowed. This procedure is elegant and not very tedious, but requires some knowledge of group theory, in particular knowledge of the connection between the irreducible representations of SU(2), SN and U(2ℓ+1) carried by N-fold tensor product spaces.
The conventional, much more tedious, non group-theoretical, way to proceed is by a "bookkeeping" procedure. Basically, one tabulates all the combinations of one-electron quantum numbers allowed by the Pauli principle and determines the combination with highest ML and MS, which are given by the respective sums of the orbit- and spin- magnetic quantum numbers of the individual electrons. This combination is unique and defines "ladders" of eigenstates with L = MLmax and S = MSmax. One removes the ladders starting with these maximum values from the table and searches for the next unique combination of highest ML and MS that are left in the table. This is repeated until the table is empty and all ladders (LS states) have been assigned.
It is of some historical interest to remark that the latter procedure was followed by Hund[4] in 1925, before the discovery of spin or introduction of Slater determinants. The following table is a combination of Tables 3 and 4 of Hund [4] (with the correction of two "bookkeeping" errors made by Hund, proving that this procedure is error prone).
| Configuration | Terms |
|---|---|
| p, p5 | 2P |
| p2, p4 | 1S, 1D, 3P |
| p3 | 2P, 2D, 4S |
| d, d9 | 2D |
| d2, d8 | 1S, 1D, 1G, 3P, 3F |
| d3, d7 |
2P, 2D, 2D, 2F, 2G, 2H, 4P, 4F |
| d4, d6 | 1S, 1S, 1D, 1D, 1F, 1G, 1G, 1I, 3P, 3P, 3D, 3F, 3F, 3G, 3H, 5D |
| d5 | 2S, 2P, 2D, 2D, 2D, 2F, 2F, 2G, 2G, 2H, 2I, 4P, 4D, 4F, 4G, 6S |
See Ref. [5] for a similar table of equivalent f electrons.
[edit] References
- ↑ H. N. Russell and F. A. Saunders, New Regularities in the Spectra of the Alkaline Earths, Astrophysical Journal, vol. 61, p. 38 (1925)
- ↑ B. R. Judd, Atomic Shell Theory Recast, Physical Review, vol. 162, pp. 28-37 (1967)
- ↑ P. E. S. Wormer, Russell-Saunders States arising from configurations of equivalent electrons, Chemical Physics Letters, vol. 5, p. 355 (1970)
- ↑ 4.0 4.1 F. Hund, Zur Deutung verwickelter Spektren, insbesondere der Elemente Scandium bis Nickel. [On the interpretation of complicated spectra, in particular the elements scandium through nickel]. Zeitschrift für Physik, vol. 33, pp. 345-371 (1925).
- ↑ C. W. Nielson and G. F. Koster, Spectroscopic Coefficients for the pn, dn, and fn Configurations, MIT Press, Cambridge, (1963).


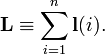
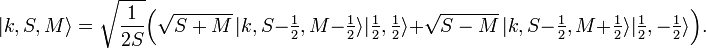

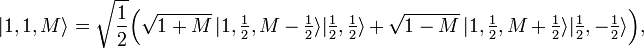
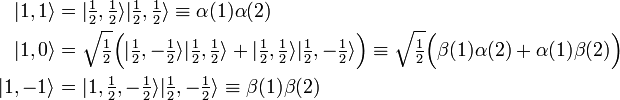
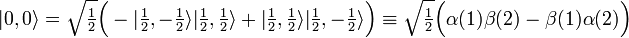
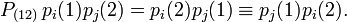
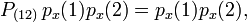
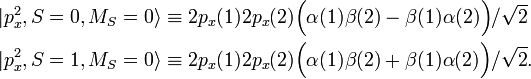
![\begin{align}
2\mathcal{A} |p_x^2, S=0, M_S = 0\rangle &= 2p_x(1) 2p_x(2) \Big( \alpha(1)\beta(2) - \beta(1)\alpha(2)\Big)/\sqrt{2} \\
& - 2p_x(2) 2p_x(1) \Big( \alpha(2)\beta(1)- \beta(2)\alpha(1)\Big)/\sqrt{2} \\
&= 2 \left[ 2p_x(1) 2p_x(2) \Big( \alpha(1)\beta(2) - \beta(1)\alpha(2)\Big)/\sqrt{2}\right]. \\
\end{align}](../w/images/math/4/9/3/4932b95abec37fccb37442aafee7f3d5.png)