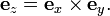Right-hand rule

The right-hand rule is a rule that appears in the cross product,

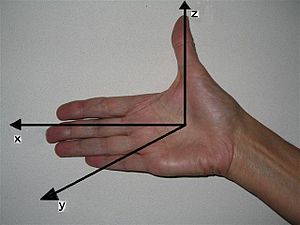
The direction of the unit vector e_z given as the cross product of unit vectors along the x- and y-axis is given by the right-hand rule, see photograph.

The case depicted here has a right (90° degree) angle α between the x- and the y-axis. However, the rule works for any angle α between x- and y-axis, as long as 0° < α < 180°. The z-axis is always perpendicular to the plane containing the x- and y-axes. If the angle α equals 0° or 180°, the cross product is the zero vector, which has an undetermined direction.