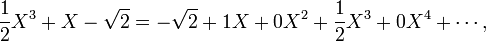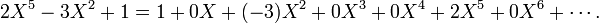Polynomial/Advanced

From Knowino

Jump to: navigation, search

In algebra, a polynomial is, roughly speaking, a formal expression obtained from constant numbers called coefficients and one or more variables by making a finite number of additions and multiplications. For instance, $x 2 - 2 x + 1$ is a polynomial involving one variable, x (often called a polynomial in one variable), whereas $x 2 + y 2$ is a polynomial in two variables, $x$ and $y$ .

In order to add and multiply polynomials, we need only know how to add and multiply their coefficients. In abstract algebra, an abstract collection of objects that can be added and multiplied subject to the usual algebraic rules is called a ring. Polynomials can be defined with coefficients from an arbitrary ring, although they will often exhibit unfamiliar properties not shared by the more common polynomials with real number coefficients. Polynomials with coefficients in an arbitrary ring form a ring themselves, with the usual addition and multiplication operations for polynomials, called a polynomial ring.

When the polynomials have coefficients in a special type of ring, called a field, then they behave in many ways similarly to polynomials with real number coefficients. Polynomials with real number coefficients are discussed on the main polynomial page. This "advanced" version discusses polynomials with coefficients in a field.

[edit] Review of fields

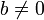A field is a set of objects, numbers if you like, which can be added and multiplied. A field contains distinct additive and multiplicative identities, denoted 0 and 1. The objects in a field can also be subtracted and divided, with the usual restriction that division by 0 is not allowed. In particular, the fraction $\frac{a}{b}$ is defined for any a and b in the field with $b \neq 0$ . Finally, we require the addition and multiplication operations to be both commutative and associative, and for multiplication to be distributive over addition. All of the usual algebraic rules for manipulating sums, differences, products, and quotients of numbers and fractions hold for the elements of a field.

[edit] Polynomials over a field

[edit] Polynomials in one variable

There are many possible equivalent approaches to defining polynomials. For instance, they can be defined as the convolution algebra of the monoid of non-negative powers of the generator X of a cyclic group. This method also allows one to define non-commuting polynomial rings, and to view polynomials in one variable as a special case. Alternatively, polynomials can be defined as infinite sequences of coefficients such that all but a finite number of coefficients are equal to zero. This approach is useful because it allows one to view a polynomial ring as a subring of a ring of formal power series. This is the approach that will be used in this article.

Let us consider some expressions like $X 2 - 2 X + 1$ , ½X ³+X−√2 , or $2 X 5 - 3 X 2 + 1$ . We can write all of them as follows:

$X^2-2X+1=1+(-2)X+1X^2+0X^3+0X^4+\cdots,$

$\frac{1}{2}X^3+X-\sqrt{2}=-\sqrt{2}+1X+0X^2+\frac{1}{2}X^3+0X^4+\cdots,$

$2X^5-3X^2+1=1+0X+(-3)X^2+0X^3+0X^4+2X^5+0X^6+\cdots.$

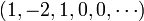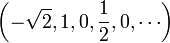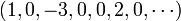This suggests that a polynomial can be entirely defined by giving a sequence of numbers, which are called its coefficients, all of them being zero from some rank. For instance the three polynomials above can be written respectively $(1,-2,1,0,0,\cdots)$ , $\left(-\sqrt{2},1,0,\frac{1}{2},0,\cdots\right)$ , and $(1,0,-3,0,0,2,0,\cdots)$ , the dots meaning the sequence continues with an infinity of zeros. This leads to the definition below.

Definition. A polynomial $P$ , over the ring $R$ is a sequence $P=\left(a_0,a_1,a_2,\cdots,a_n,\cdots\right)$ of elements of $R$ , called the coefficients of $P$ , this sequence containing only a finite number of nonzero terms. The rank of the last nonzero term is called the degree of the polynomial.

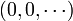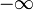Hence, the degrees of the three polynomials given above are respectively 2, 3 and 5. By convention, the degree of $(0,0,\cdots)$ is set to $-\infty$ .

This definition may surprise the reader, because in reality, one thinks of a polynomial as an expression of the form 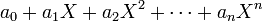$a_0+a_1X+a_2X^2+\cdots+a_nX^n$ rather than 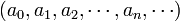$\left(a_0,a_1,a_2,\cdots ,a_n,\cdots\right)$ . We will progressively show how to return to this usual way of writing a polynomial. First, we identify any element $a 0$ of the ring to the polynomial 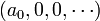$\left(a_0,0,0,\cdots\right)$ . 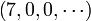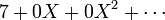For instance, we write only $7$ instead of the cumbersome $\left(7,0,0,\cdots\right)$ , (or in the familiar fashion $7+0X+0X^2+\cdots$ ).

Secondly, we merely denote by $X$ the polynomial

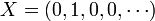$X=\left(0,1,0,0,\cdots\right)$ .

This is natural, as in the familiar fashion this sequence corresponds to 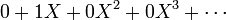$0+1X+0X^2+0X^3+\cdots$ It remains to give a sense to $X 2$ , $X 3$ , etc. This will be made in the next two subsections.

[edit] Polynomials in several variables

[edit] Operations

We now define addition and multiplication of polynomials.

[edit] Addition

With the traditional notation, if we have $P = 2 X 5 - 3 X 2 + 1$ and $Q = - X 5 + 4 X 4 + 2 X 2 - 1$ , we want to have $P + Q = (2 - 1) X 5 + 4 X 4 + ( - 3 + 2) X 2 + 1 - 1 = X 5 + 4 X 4 - X 2$ , that is, one wants to add coefficients separately for each degree. This leads to the formal definition below.

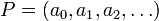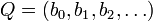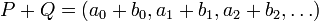Definition. Given two polynomials $P=\left(a_0,a_1,a_2,\dots\right)$ and $Q=\left(b_0,b_1,b_2,\dots\right)$ , the sum $P + Q$ is defined by $P+Q=\left(a_0+b_0,a_1+b_1,a_2+b_2,\dots\right)$ .

[edit] Multiplication

Multiplication is harder to define. Let us begin with an example using traditional notation. For $P = X 2 + X - 2$ and $Q = 2 X 2 - 3 X + 1$ , we want to have

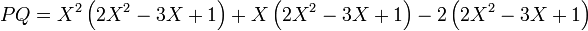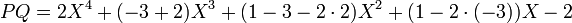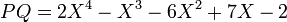$PQ=X^2\left(2X^2-3X+1\right)+X\left(2X^2-3X+1\right)-2\left(2X^2-3X+1\right)$ ; $PQ=2X^4+(-3+2)X^3+(1-3-2\cdot 2)X^2+(1-2\cdot (-3))X-2$ ; $PQ=2X^4-X^3-6X^2+7X-2 \$ .

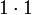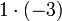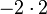One can observe that the coefficient of say, $X 2$ , is obtained by adding $1\cdot 1$ , $1\cdot (-3)$ and $-2\cdot 2$ , that is, by adding all the $a i b j$ so that $i + j = 2$ , where the $a i$ denote the coefficients of $P$ and the $b j$ those of $Q$ . Those mechanics lead to give the definition below.

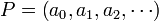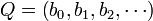Definition. Given two polynomials $P=\left(a_0,a_1,a_2,\cdots\right)$ and $Q=\left(b_0,b_1,b_2,\cdots\right)$ , the product $P Q$ is defined by 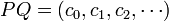$PQ=\left(c_0,c_1,c_2,\cdots\right)$ , where for every index $k$ , the coefficient $c k$ is given by

c_k =	∑	a_ib_j
	i + j = k

.

The reader which is upset by those cumbersome notations should just retain that this definition allows to multiply polynomials (considered as mere sequences of coefficients) as one is used to do in elementary algebra (using the traditional notation, as in the example). The only striking fact is that in our construction, $X$ does not represent a number, but a pure abstract entity for which we have defined some rules of calculation.

[edit] The algebra $R [X]$

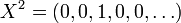With the definition above, one can verify that the product of the polynomial $X=\left(0,1,0,0,\dots\right)$ by itself, that is $X 2$ , is the sequence $X^2=\left(0,0,1,0,0,\dots\right)$ . More generally, for each natural number $n$ , one can verify that the $n$ -th power of $X$ is given by 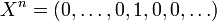$X^n=\left(0,\dots,0,1,0,0,\dots\right)$ , where the $1$ is the coefficient of index $n$ and all other coefficients are zeros. In particular, we have the usual convention 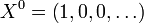$X^0=\left(1,0,0,\dots\right)$ , which we identified to the constant $1$ .

Now, any polynomial 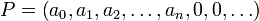$P=\left(a_0,a_1,a_2,\dots,a_n,0,0,\dots\right)$ is exactly equal to 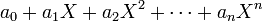$a_0+a_1X+a_2X^2+\cdots+a_nX^n$ , where the addition and the powers (which are mere repetitions of multiplications) are defined as in the preceding subsections. Our whole construction legitimates the traditional notation, and from now on, we will only use the later, with which calculations use natural rules of elementary algebra. It is however important to remember that the "variable" $X$ did not denote some number in our construction, but a particular sequence of coefficients. We have succeeded in defining polynomials in a purely formal manner.

[edit] Operations and degree: the algebra $R n [X]$

[edit] Polynomials versus polynomial functions

It may be convenient to think of a polynomial as a function of its variables, that is, 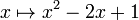$x\mapsto x^2-2x+1$ or $(x,y)\mapsto x^2+y^2$ . Such a function is called a polynomial function. But in reality, both concepts are different, the unspecified variables being purely formal entities when one thinks of an abstract polynomial, whereas they are meant to be replaced by any number when one thinks of a function. The distinction is important in abstract algebra, because what we have called "constant numbers" is more generally replaced by any ring, and for some rings the two concepts cannot be identified. There is not such a problem with polynomials over rings of usual numbers like integers, rational, real or complex numbers. Still it is important to understand that calculations with polynomials can be conceived in an only formal way, without giving any special ontological status to the variables. To make the distinction clear, it is common in algebra to denote the abstract variables with capital letters ( $X$ , $Y$ , etc.), while variables of functions are still denoted with lowercase letters. We will use this convention in what follows.

Polynomial/Advanced

Contents

[edit] Review of fields