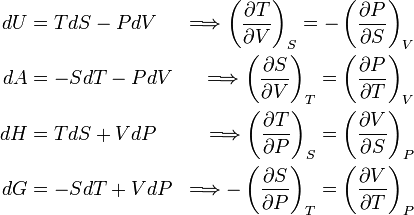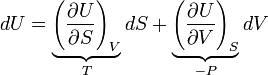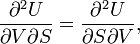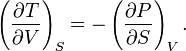Maxwell equations (thermodynamics)
From Knowino
In thermodynamics, the Maxwell equations are a set of equations derived by application of Euler's reciprocity relation to the thermodynamic characteristic functions. The Maxwell relations, first derived by James Clerk Maxwell, are the following expressions between partial differential quotients:
The characteristic functions are: U (internal energy), A (Helmholtz free energy), H (enthalpy), and G (Gibbs free energy). The thermodynamic parameters are: T (temperature), S (entropy), P (pressure), and V (volume).
As an example of a derivation, consider
Euler's reciprocity relation reads:
which indeed gives