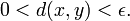Limit point

In topology, a limit point (or "accumulation point") of a subset S of a topological space X is a point x that cannot be separated from S.

Contents 1 Definition 1.1 Metric space 2 Properties 3 Derived set 4 Related concepts 4.1 Limit point of a sequence 4.2 Adherent point 4.3 ω-Accumulation point 4.4 Condensation point 5 References

[edit] Definition

Formally, x is a limit point of S if every neighbourhood of x contains a point of S other than x itself.

A limit point of S need not belong to S, but may belong to it.

[edit] Metric space

In a metric space (X,d), a limit point of a set S may be defined as a point x such that for all ε > 0 there exists a point y in S such that

This agrees with the topological definition given above.

[edit] Properties

• A subset S is closed if and only if it contains all its limit points.
• The closure of a set S is the union of S with its limit points.

[edit] Derived set

The derived set of S is the set of all limit points of S. A point of S which is not a limit point is an isolated point of S. A set with no isolated points is dense-in-itself. A set is perfect if it is closed and dense-in-itself; equivalently a perfect set is equal to its derived set.

[edit] Related concepts

[edit] Limit point of a sequence

A limit point of a sequence (a_n) in a topological space X is a point x such that every neighbourhood U of x contains all points of the sequence with numbers above some n(U). A limit point of the sequence (a_n) need not be a limit point of the set {a_n}.

[edit] Adherent point

A point x is an adherent point or contact point of a set S if every neighbourhood of x contains a point of S (not necessarily distinct from x).

[edit] ω-Accumulation point

A point x is an ω-accumulation point of a set S if every neighbourhood of x contains infinitely many points of S.

[edit] Condensation point

A point x is a condensation point of a set S if every neighbourhood of x contains uncountably many points of S.

[edit] References

• Wolfgang Franz (1967). General Topology. Harrap, 23. 
• Lynn Arthur Steen; J. Arthur Seebach jr (1978). Counterexamples in Topology. Berlin, New York: Springer-Verlag, 5-6. ISBN 0-387-90312-7. 

Some content on this page may previously have appeared on Citizendium.