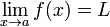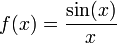Limit of a function
In mathematics, the concept of a limit is used to describe the behavior of a function as its argument either "gets close" to some point, or as it becomes arbitrarily large.
Suppose f(x) is a real-valued function and a is a real number. The expression
means that f(x) can be made arbitrarily close to L by making x sufficiently close to a. We say that "the limit of the function f of x, as x approaches a, is L". This does not necessarily mean that f(a) is equal to L, or that the function is even defined at the point a.
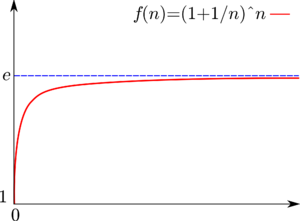
Limit of a function can be defined at values of the argument at which the function itself is not defined. For example,
although the function
is not defined at x=0.
[edit] Formal definition
Let f be a function defined (at least) on some open interval containing a (except possibly at a) and let L be a real number. Then the equality
means that
- for each real ε > 0 there exists a real δ > 0 such that all x with 0 < |x − a| < δ satisfy |f(x) − L| < ε.
This formal definition of function limit is due to the German mathematician Karl Weierstrass.
[edit] See also
| |
Some content on this page may previously have appeared on Citizendium. |