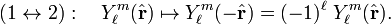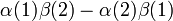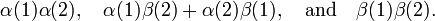Hydrogen

Hydrogen is a chemical element with atomic number Z = 1 and chemical symbol H. It is the most abundant element in the universe, (about 90% in number of atoms, about 70% in mass). It exists primarily in interstellar gas clouds and stars, but it is also thought that hydrogen is a major component of the planet Jupiter. On earth hydrogen is mainly bound to other elements, to carbon in carbohydrates and hydrocarbons, to oxygen in water, and to nitrogen in ammonia. Measured in number of atoms, hydrogen is the third abundant element (15%) on earth. Atomic hydrogen is very reactive and does not naturally appear in free form. The hydrogen molecule H₂ is a stable gas at ambient temperature and pressure.

[edit] Isotopes

The hydrogen atom has two stable and one unstable isotope. Its average (weighted by abundance) mass is 1.00794 u. Only protium (¹H) and deuterium (²H = D) occur in sizeable quantities in nature. The isotope tritium (³H = T) is largely man-made and is unstable with a half-life of about 12.3 years. Its nucleus contains one proton and two neutrons. It decays into ³He releasing beta particles.

Masses (in unified atomic mass unit u), and abundances (percentage in brackets) are:

¹H   1.0078250321 (99.9885%)

²H   2.0141017780 (0.0115%)

³H   3.0160492675 (10⁻¹⁵%)

Isotope data from Ref. ^[1].

[edit] Physical properties

Under normal temperature and pressure H₂ is a colorless, tasteless, and odorless gas. The most commonly occurring hydrogen molecule is diatomic (H₂) and has a boiling point of 20.28 K and a melting point of 14.01 K. For the deuterium molecule these temperatures are about 4 K higher: D₂ has boiling point 23.65 K and melting point 18.65 K.

At ambient temperature and pressure the density of gaseous hydrogen is 0.08988 kg/m³. The density of the liquid (at boiling point) is 70.8 kg/m³ and the density of the solid is 70.6 kg/m³ (at 11 K).

The triple point is at temperature 13.81 K with a pressure 7.042 kPa. The critical point is at 33.15 K, 1.298 MPa. The critical density is 30.09 kg/m3.

[edit] Ortho/para hydrogen

Results of measurements of the specific heat C_v of gaseous ¹H—¹H can be interpreted by assuming a 3:1 mixture of two species (so-called spin isomers) of hydrogen: ortho (parallel proton spins) and para (antiparallel proton spins) hydrogen. The difference between the two spin isomers is of purely quantum mechanical nature and has no classical explanation. The now following exposition assumes some basic knowledge of quantum mechanics; readers who lack this are advised to skip the remainder of this section.

Even for temperatures much higher than room temperature (300 K), the hydrogen molecule is in its vibrational and electronic ground state. The first vibration excitation energy is 4358 cm⁻¹, which corresponds to an energy of 6270 kT. This means that for temperatures well below 6000 K the molecule has effectively only rotational and translational degrees of freedom. Except for extremely low temperatures, the translation of the molecule can be described by classical physics. Very close to the absolute zero (mK or less) cooperative quantum effects, like Bose-Einstein condensation, will affect the translational motion, but since we will consider higher temperatures (say from 40 K to 300 K), we can safely ignore those. Hence, from a quantum physics point of view the hydrogen molecule is a linear rigid rotor—at least in the broad temperature range of interest.

It is known that the rotational wave functions of a linear rigid rotor are spherical harmonics , where 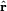is a unit vector pointing from nucleus 1 to nucleus 2. Interchange of the two identical nuclei in ¹H—¹H reverts the direction of this vector and has the following effect on the rotational wave function:

That is, wave functions of odd 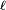are antisymmetric and of even 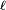are symmetric under exchange of the nuclei (protons in this case). The two nuclei in ¹H—¹H are spin-½ particles (fermions) and are subject to the Pauli postulate that requires their total (rotational times spin) wave function to be antisymmetric. The spin part of the protonic wave function is either spin-singlet:

or spin-triplet, with—as the name suggests—three functions:

Note that the singlet is antisymmetric (changes sign) and the triplets are symmetric (stay the same) under the interchange of the proton spin coordinates (indicated by 1 and 2). So, in order to satisfy the Pauli postulate, rotational functions of even 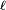must be combined with spin singlets, while functions of odd 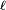must be combined with spin-triplets. The hydrogen molecule in an even-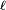, spin-singlet, state is known as para hydrogen. The hydrogen in an odd-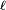, spin-triplet, state is known as ortho hydrogen.

Since the rotational energy of a linear rotor is 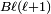, where B is the rotational constant, it follows that ortho and para hydrogen have a different energy spectrum and hence different Boltzmann distributions (partition functions). The concentrations of the two species in equilibrium are determined by Boltzmann averaging and are accordingly temperature dependent. It can be shown that at room temperature (300 K) the concentration ratio is in the high temperature limit, which is 3:1 (due to the spin triplet/singlet ratio). The equilibrium ratio shifts towards increasing concentrations of para hydrogen for decreasing temperatures, because para hydrogen has zero as its lowest energy (for 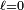), whereas ortho hydrogen has 2B > 0 (for 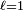) as its lowest energy. However, the equilibrium ratio is not what is observed in measurements below 300 K down to, say, 40 K. It turns out that the ortho-para conversion is very slow (it is a spin-forbidden transition), so that the ratio 3:1 is preserved when one cools down a gas that was in equilibrium at 300 K. This means that at lower temperatures the gas is not in equilibrium but in a metastable state with the fixed ratio 3:1 between ortho and para hydrogen. The rules of statistical mechanics (Boltzmann averaging etc.) are still applicable if one considers the gas as a binary 3:1 mixture of two different species. Doing this, the observed specific heat C_v as function of temperature can be completely understood.

[edit] Solid state

Upon coooling to freezing point, normal hydrogen H₂ and deuterium D₂ form molecular (diatomic) crystals in a hexagonal-closed-packed (hcp) structure. In this behavior hydrogen resembles the halogens and not the alkalis, which crystallize into atomic metals. Ortho-hydrogen transforms to a face-centered cubic lattice on cooling to 2.8 K, unless it has been converted to pure parahydrogen, which retains the hcp structure. In 1935 it was suggested by Wigner and Huntington that solid hydrogen will become an atomic alkali-like metal under very high pressure. They estimated this transition at zero degree kelvin to be at a pressure of around 25 GPa (0.25 Mbar). However, metallic hydrogen has not yet been observed to date and it is now thought that the required static pressure may exceed 600 GPa (6 Mbar).^[2]

[edit] Chemical properties

The neutral atom has nuclear charge e (the elementary charge) and one electron (charge −e). The electronic wave functions of the ground and excited states of the H-atom are known exactly, because the Schrödinger equation can be solved analytically for one-electron atoms, see hydrogen-like atoms. In the ground state the electron is in a 1s orbital (a nodeless spherically symmetric function with energy -13.59 eV).

The molecule H₂ has an equilibrium distance r_e = 1.4011 bohr, an equilibrium energy D_e: 38 297.1 cm⁻¹ (458.135 kJ/mol) and a dissociation energy D₀: 36118.069 cm⁻¹ (is 432.068 kJ/mol, the energy for dissociation from the vibrational ground state).^[3] Because of this relatively high binding energy, molecular hydrogen is fairly inert. Many reactions of hydrogen require high temperatures and a catalyst.

Hydrogen resembles alkali metals, like Li and Na, in that it can lose its (outer) electron and become the cation H⁺. Strong acids, dissolved in water, dissociate and release H⁺, for instance HCl → Cl⁻ + H⁺. Note, however, that the free hydrogen nucleus, being a bare charge, will not remain free in solution, but will immediately associate with solvent molecules, e.g., with water it will associate to H₃O⁺.

Hydrogen also resembles halogens, like Cl, in that it can form an anion. It does so in saline hydrides (LiH, NaH, CaH₂, etc.), in which to a large extent the binding is ionic, i.e., it is of the type M⁺–H⁻. These compounds are solids with a high melting point.

Hydrogen also forms bonds that are mainly covalent, as in carbohydrates, water, and ammonia.

Hydrogen gas is highly flammable and will burn already at low concentrations in air with an almost invisible flame (its color being mainly in the UV). It combusts according to the following exothermic equation (at constant pressure):

2 H₂(g) + O₂(g) → 2 H₂O(l)

where the enthalpy of reaction ΔH is −571.6 kJ^[4] (per mole O₂).

[edit] Preparation

A classical way of preparing hydrogen in a laboratory is by pouring sulphuric acid on zinc:

H₂SO₄ + Zn → ZnSO₄ + H₂

As was already known by Henry Cavendish in the second half of the 18^th century, zinc may be replaced in this recipe by iron or tin and sulphuric acid by hydrochloric acid (HCl in water).

Another way of preparing hydrogen gas is by immersing aluminum trimmings in a solution of sodium hydroxide in water:

2Al + 2NaOH + 2H₂O → 2NaAlO₂ + 3H₂.

This reaction runs violently.

In the electrolysis of water two oppositely charged electrodes are immersed into vessel filled with water. The negative electrode (the cathode) and the positive electrode (the anode) are kept at a voltage difference of at least 0.83 V. In non-acidic water the following reaction occurs at the cathode:

4H₂O + 4e⁻ → 2H₂ + 4OH⁻.

Sometimes water is electrolyzed that is made slightly acidic by the solution of sulphuric acid, the reaction at the cathode is then:

4H₃O⁺ + 4e⁻ → 2H₂ + 4H₂O.

The OH⁻ (and in acidic solution also SO₄⁻) anions move to the anode. The hydroxyl anion decomposes before the sulphate anion according to

4OH⁻ → O₂ + 2H₂O + 4e⁻,

so that there is a closed cycle of charge transport: in the water from cathode to anode carried by anions and outside the water back from anode to cathode by electrons driven by an external power source (for instance a battery). The formation of gaseous hydrogen is at the cathode, while gaseous oxygen is formed at the the anode. This process, which requires electrical power to keep on cycling, is energetically not very efficient and at present not economically competitive with steam reforming of natural gas (CH₄).

On a large, industrial scale, steam reforming of natural gas (SMR—steam methane reforming) water vapor reacts with methane to yield carbon monoxide and H₂ at high temperatures (700 – 1000 °C),

CH₄ + H₂O → CO + 3 H₂.

This process takes place under 3-25 bar pressure (1 bar = 100 kPa = 0.987 atm) in the presence of a nickel oxide catalyst. SMR is endothermic—that is, heat must be supplied to the process for the reaction to proceed. The product mixture is known as synthesis gas ("syngas") because it is often used directly for the production of methanol and related compounds. Hydrocarbons other than methane can be used to produce synthesis gas

C_xH_y + x H₂O → x CO + (x + 0.5y) H₂,

but steam reforming of heavier hydrocarbons has the problem that it gives pure carbon (coke) as a contaminating byproduct. The steam reforming of methane is by far the largest source of hydrogen gas today.

With the use of an iron oxide catalyst it is possible to generate hydrogen by the water-gas shift reaction, which is slightly exothermic,

CO + H₂O → CO₂ + H₂

and removes the carbon monoxide from the gas mixture. The carbon dioxide can be frozen out from the product mixture or can be washed out by a solution of KCO₃ in water.

[edit] Usage

It is expected by some people that, in the future, hydrogen will replace gasoline as a fuel for cars and trucks (in the so-called hydrogen economy). At this moment the main use of hydrogen is in the manufacturing of ammonia by catalytic reaction of hydrogen with nitrogen (Haber-Bosch process—the most important nitrogen fixation process). The produced ammonia is used for the manufacturing of nitrogen-containing fertilizers.

Another important application of H₂ is hydrocracking. This is a catalytic cracking process of heavy hydrocarbons in the presence of hydrogen to lighter, more desirable, hydrocarbons. Hydrogen prevents the formation of polycyclic aromatic compounds. Another important role of hydrogen in the cracking is the reduction of tar formation and the prevention of buildup of coke on the catalyst. Hydrogenation also converts sulfur and nitrogen atoms present in the feedstock to hydrogen sulfide and ammonia, which can easily be removed from the product. The products of hydrocracking are saturated hydrocarbons ranging from ethane, LPG to high-octane gasoline.

Other use of hydrogen is in high temperature welding. Further, it is used as rocket fuel. Since the density of air is about 15 times that of hydrogen, (the molecular mass of hydrogen being about 1/15 of that of nitrogen and oxygen), hydrogen is a good gas for balloons. However, since it is very inflammable, it is not used to lift people, but it is regularly used in weather balloons.

Hydrogen's isotopes also have applications. Deuterium (D = ²H) in the form of heavy water (D₂O) is used in nuclear reactors as a moderator to slow down neutrons. Deuterated compounds have applications in chemistry and biology in studies of isotope effects in molecules. Tritium (³H), produced in nuclear reactors, is used in hydrogen bombs.

Liquid hydrogen is important in cryogenics and in the study of superconductivity, as its boiling point is only 20.28 degrees above absolute zero.

[edit] History

It is not completely clear who discovered hydrogen. Some say it was Paracelsus (Theophrastus Bombastus von Hohenheim, 1492—1541), but others deny it.^[5] The first (1670) written source is by Robert Boyle in his New Experiments touching the Relation between Flame and Air, where he describes the escape of inflammable "fumes" when hydrochloric acid is poured over iron filings. A century later it was well-known among chemists that hydrochloric acid as well as sulphuric acid react with different metals to give "inflammable air" (as Henry Cavendish called hydrogen gas). The relation of the gas with water was not known, however, until 1783 when Cavendish proved that "dephlogisticated air" (air without phlogiston, i.e, oxygen gas) reacts with "inflammable air" giving water only. This result was communicated to Lavoisier, who repeated the experiment and presented it to the Académie Royale des Sciences, also in 1783. Lavoisier coined the name hydrogen—generator of water. He modeled this after the old-Greek prefix hydr (ὑδρ) in many compound words meaning water, for instance ὑδροφόρος, water carrying.

James Dewar liquified hydrogen in 1898 and crystallized it a year later (1899).

[edit] References

1. ↑ NIST
2. ↑ W. J. Nellis, Metastable solid metallic hydrogen, Philosophical Magazine B, 1999, vol. 79, pp. 655-661 (1999).
3. ↑ L. Wolniewicz, J. Chem. Phys. vol. 103, pp. 1792-1799 (1995)
4. ↑ E. A. Guggenheim, Thermodynamics, 5th edition, North Holland, Amsterdam (1967), p. 242
5. ↑ J. M. Stillman, The Story of Alchemy and Early Chemistry, Dover, New York (1960)