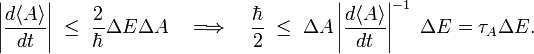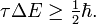Heisenberg uncertainty principle
In quantum mechanics, the Heisenberg uncertainty relations, named after their discoverer Werner Heisenberg,[1] state that pairs of certain physical quantities cannot be measured simultaneously with arbitrarily small error. Even when a quantum mechanical system is in a well-defined state, a pair of its canonically conjugate properties cannot be determined simultaneously with arbitrary certainty. The best-known canonically conjugate pairs for which Heisenberg's uncertainty relations are valid are the components of position r = (x, y, z) and of momentum p = (px , py , pz ) of a particle. The uncertainties (root-mean-square deviations), indicated by Δ, satisfy the inequalities
where h is Planck's constant.
It is one of doctrines of quantum mechanics that identical measurements of an observable property 𝒫 performed on identical physical systems S in identical states ψ do not necessarily result in the same values for 𝒫, but commonly yield a certain spread Δ𝒫 ≥ 0 in measured values. Likewise, another observable 𝒬 measured many times on the same system S in the same state ψ will show a spread Δ𝒬 in the results. The occurrences of these basic indeterminacies in quantum mechanics caused many physicists, among whom some of its founders, Albert Einstein, Erwin Schrödinger and Louis de Broglie, to believe that quantum mechanics is only a transitional theory in wait for a better—determinate—theory.
When the observables 𝒫 and 𝒬 are canonically conjugate, that is, when their commutator[2] satisfies 𝒫𝒬−𝒬𝒫 = h/(2πi), then the Heisenberg uncertainty principle states that the product of the two spreads obtained from system S in state ψ satisfy the inequality Δ𝒫Δ𝒬 ≳ h/(4π). A narrow spread Δ𝒫 ≈ 0, meaning that the results of the measurements of 𝒫 are closely spaced around an average value ⟨𝒫⟩, implies a large spread Δ𝒬, i.e., measurements of 𝒬 yield widely scattered results.
Returning to the Heisenberg relations for the pairs (x, px), (y, py), and (z, pz), we see that the more precisely the components of the position r of a particle are determined, the more uncertain are the corresponding components of its momentum p. Conversely, if a particle with mass m has a well-defined ("sharp") velocity v = p/m, its position r is completely undetermined; the particle can be found everywhere in space with equal probability (is a plane wave). In other words, the Heisenberg uncertainty principle states that locating a particle in a small region of space makes the momentum of the particle uncertain; and conversely, that preparing the particle in a state of precise momentum makes the position uncertain.
There is another, less strict, quantum mechanical inequality regarding time and energy, that is also due to Heisenberg,
Here τ is an "uncertainty" in time and ΔE is the RMS deviation in energy. In non-relativistic quantum mechanics time is not an observable, but a parameter and the RMS deviation Δt is zero. Usually one takes for τ something like a lifetime of a metastable system, the duration of a collision of two particles, or the time it takes an atom to absorb a photon.
Contents |
[edit] Heisenberg's uncertainty relation for p and q
[edit] Root-mean-square deviation
A measure for the uncertainty in a set of observations is the root-mean-square deviation (RMS deviation, also known as standard deviation). If n values x1, x2, ..., xn of a quantity x have been measured then the variance (Δx)2 is the sum of residuals squared,
It is follows that
Introducing the following notation
and taking the positive square root, it follows that the RMS deviation (standard deviation) is
[edit] RMS deviation in quantum mechanics
In quantum mechanics the RMS deviation Δx has the same definition, provided one defines
where ψ is a wave function normalized to unity. The bra-ket ⟨ .. ⟩ stands for an integral over an appropriate configuration space; for a free particle moving in one dimension the configuration space is the real axis. This definition of ⟨A(x)⟩ relies on the interpretation of |ψ|2 as a probability (weight) function. In quantum mechanics the function A(x) represents usually a physical quantity, an observable. As pointed out in the introduction, one of the tenets of quantum mechanics is that identical measurements of A(x) performed on replicas of a system (identical systems with identical wave functions ψ) give different answers. The experimental data show a statistical distribution described by the weight function |ψ|2 and the root-mean-square deviation:
Note the special case: if ψ is an eigenfunction of the observable A(x) then
and
In case the system is in an eigenstate of A, the outcome of measurements of A give all the same answer α, the eigenvalue α. It is to be expected that ΔA is small, close to zero, when ψ does not deviate too far from an eigenfunction of A.
As pointed out above, Heisenberg's uncertainty relation for a particle moving along the x-axis is
In accordance with the general definition the uncertainties are
The symbol ≳ means that, although the left-hand side is always greater than the right-hand side, there are cases where the left-hand side is as good as equal to the right-hand side. Equality occurs for Gaussian-type (bell-shaped) wave functions ψ. For other wave functions the product ΔpxΔx is often not much larger than h/(4π).
Clearly, when Δpx shrinks, Δx has to grow larger and larger in order to satisfy the Heisenberg inequality. For example, a plane wave ψ(x) = exp[2πipx/h] is an eigenfunction of p = − ih/(2π) d/dx, so that Δpx = 0; a plane wave particle has a position x that is completely undetermined. Conversely, if the position of the particle is very well determined, its momentum is very uncertain. The p-expansion (Fourier transform) of a well-localized wave packet (Δx ≈ 0) requires eigenstates of many different eigenvalues p and hence gives rise to a large spread in p.
[edit] Example: small macroscopic particle
Because h is a very small number (6.6×10−34 J⋅s) the uncertainty in position and momentum is negligible for macroscopic particles, even for dust particles of the size of a micrometer (= 10−6 m).
A numerical example, performed in SI units, may illustrate that the Heisenberg relation is irrelevant for a macroscopic particle, even for a very small one. Take a spherical dust particle of diameter d = 2⋅10−6 m moving in one direction, the x direction. Its volume is 4π/3 ⋅ (d/2)3 ≈ 4.2× 10−18 m3. If the specific density of the material constituting the particle is, say, five times that of water, then it is 5×103 kg/m3 and the dust particle has mass
- m = 2.1×10−14 kg.
If the particle floats around with
- vx = 1 mm/s = 10−3 m/s,
then its momentum is
Say the position of the dust particle is known with a root mean square (RMS) deviation that is one percent of its diameter,
- Δx = 2×10−8 m.
Then the RMS deviation in the momentum obeys
which may be compared to the absolute value px = 2.1⋅10−17 J s/m, i.e., the RMS error of px has the bound that it must be larger than 10−10 of its absolute value. A possible error in the tenth decimal digit of px is completely undetectable and the conclusion must be that the bound imposed by the laws of quantum mechanics on Δpx is irrelevant for the macroscopic dust particle.
[edit] Example: Bohr's hydrogen atom
In 1913 Niels Bohr posited a model for the hydrogen atom that is transitional between classical and quantum mechanics. Not only in time (halfway between Planck's introduction of the constant h named after him in 1900 and the formulation of quantum mechanics in 1925/1926), but also in concepts. Bohr postulated, following Ernest Rutherford, that the electron in the hydrogen atom circles the nucleus like the planets circle the Sun. Certain of the Bohr orbits (those with maximum azimuthal quantum number k) are circular, others are elliptic. Bohr's quantization condition is:
where ℓz is the z-component of the angular momentum of the electron moving in a circular orbit contained in the x-y plane and ℏ = h/(2π). The kinetic plus potential energy of the electron in the Bohr orbit is
where R is the Rydberg constant and c the speed of light. Note that the electronic energy increases, becomes less negative, with increasing k. High (k >> 1) values correspond to highly excited states.
It is of interest to investigate whether Bohr's electron can be seen as a classical particle, in the sense that its position r and momentum p are simultaneously well-defined ("sharp"), or that it is a quantum mechanical particle of which the two observables p and r cannot be sharp simultaneously. In order to answer this question, the relative error in the product pr will be investigated.
The classical expressions for a particle in a circular orbit with angular velocity ω are
so that
Further
hence Bohr's theory yields that the product pr is quantized,
If the particle is classical, the relative uncertainties (which are positive) are small, satisfying
and it follows that the electron may be said to move classically if
that is, when pr is much larger than ΔpxΔx.
The Bohr quantization condition states that pr grows linearly with k and when the RMS errors are assumed to be more or less independent of k (somewhat larger than ℏ), it follows from the Heisenberg relation that the relative uncertainty in pr goes to zero with increasing k,
while for small k, say k = 2,
representing a large relative uncertainty in pr (about twenty-five percent error).
From the point of view of the Heisenberg uncertainty relation, the electron in a low-energy—small k—state of the Bohr hydrogen atom is a quantum mechanical particle with a RMS error in pr that has the same order of magnitude as pr itself. For highly excited energy states the electron orbit has a small (relative to pr) spread in momentum and position. For large k the electron is more like a classical particle, characterized by a small relative error in pr, while for small k it is a quantum particle.
[edit] Derivation of the Heisenberg relation for p and q
First it will be shown that for arbitrary Hermitian operators A and B the following inequality holds:[3]
As a preliminary it is recalled that the expectation value of a Hermitian operator (H† = H) is real, while that of an anti-Hermitian operator (A† = −A) is purely imaginary, namely,
where the superscript ∗ stands for complex conjugation. This means that the expectation value ⟨G⟩ of an arbitrary linear operator G can be decomposed in a real and imaginary part as follows,
from which follows that
The derivation of the inequality, Eq. (1), above is based on the Schwarz inequality,
The equality sign holds if and only if Φ and Ψ are proportional.
Define new Hermitian operators and their action on an arbitrary function ψ normalized to unity. The expectation values in the next equation are with respect to the same ψ:
By the Schwarz inequality,
Further, using (AB)† = BA,
It is easy to see that
so that
Since
it follows a fortiori that
As shown earlier,
and the same for operator B. Hence for arbitrary Hermitian operators A and B it holds that
from which the inequality, Eq. (1), to be proved follows.
The inequality just proved is not very interesting when the right-hand side is zero, because then it states that the product on the left-hand side is greater than, or equal to, zero, which was already known (the RMS deviations are positive or zero). The right-hand side is zero for any ψ when A and B commute, that is if [A,B] = 0. But it can also be zero for certain ψ and non-zero commutator. An example of the latter is found in the theory of angular momentum where one has
The inequality becomes interesting when the commutator is a constant c times the unit operator. Then the product of standard deviations on the left-hand side is greater than, or equal to, the absolute value |c| for any normalized ψ. This is the case for px and x where c = −iℏ,
The Heisenberg uncertainty relation follows immediately for any normalized ψ,
Finally, it is of interest to consider whether the equality sign in the Heisenberg relation can occur. Let us return to Eq. (2) and assume that we can choose
Because of the proportionality of the functions, Schwarz's inequality in Eq. (2) becomes an equality,
Now
so that, when the proportionality holds, Eq. (2) becomes,
Consider now
where the normalization constant N of the Gauss function is chosen such that ⟨ψ|ψ⟩=1. Then
So that, indeed, proportionality is possible,
and the equality may be applied,
or, taking square roots and substituting the commutator,
It is reasonable to assume that for wave functions that are similar to Gauss functions, the Heisenberg relation is
[edit] Heisenberg's uncertainty relation for time and energy
- The formulation of the time-energy uncertainty relation given in this section is due to Leonid Isaakovich Mandelstam and Igor Yevgenyevich Tamm.[4]This section follows the treatment of A. Messiah.
For time-dependent processes one must consider time-dependent wave functions ψ(t) that are solutions of the time-dependent Schrödinger equation
where H is the energy operator, a Hermitian operator (an observable). It is assumed that there are no time-dependent external fields, so that H is independent of time t. It is easy to prove that the norm ⟨ψ(t)|ψ(t)⟩ is time-independent; it will assumed to be equal to one. Since the forming of bra-ket (integral over configuration space) does not involve an integration over t, one has
Because of this vanishing, one must search for another measure of uncertainty in time. Consider to that end the rate of change of the expectation value of a time-independent observable A. Consider a time interval t2−t1= τA such that
that is, in the interval τA the expectation value of A has changed in absolute value by the RMS deviation ΔA. (In taking the integral it was assumed that the rate of change is constant over the interval τA). Since during the interval τA the observable A undergoes the change ΔA, the interval τA is a reasonable unit for measuring changes over time in ⟨A⟩.
It is easy to give a quantum mechanical expression for the rate of change,
and hence,
By Eq. (1),
where ΔE ≡ ΔH. From this
Different observables A have different values for τA, assume that there is a smallest, call it τ and it follows finally that
This inequality is often used somewhat loosely. For instance, in molecular spectroscopy one identifies τ often with the lifetime of an excited state. In spectroscopy, where photons are observed that are emitted from an excited state, one concludes from sharp spectral lines (small ΔE) that the lifetime of the excited state is large. Conversely, short-lived excited states give broad spectral lines.
[edit] Notes and references
- ↑ W. Heisenberg, Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik [On the conceptual content of the quantum theoretical kinematics and mechanics], Zeitschrift für Physik, Vol. 43, pp. 172–198, DOI
- ↑ The observable properties 𝒫 and 𝒬 are identified with their Hermitian operators acting on state space.
- ↑ H. P. Robertson, The uncertainty principle, Physical Review, vol. 34, pp. 163–164 (1929). DOI
- ↑ L. Mandelstam and I. Tamm. J. Phys. (USSR) vol. 9 , pp. 249-254 (1945) Russian text.
Any book on quantum mechanics treats the uncertainty relations. Two of such books, both translated from the French, are
- A. Messiah, Quantum Mechanics, vol. I, North Holland, Amsterdam (1967)
- C. Cohen-Tannoudji, B. Diu, and F. Laloë, Quantum Mechanics, vol. I, John Wiley, New York (1977).



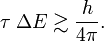
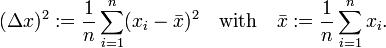
![\begin{align}
(\Delta x)^2 &=
\frac{1}{n} \left[ \sum_{i=1}^n x_i^2
+\;\bar{x}^2 \sum_{i=1}^n 1\; - 2\bar{x} \sum_{i=1}^n x_i \right] \\
&= \frac{1}{n}\left[ \sum_{i=1}^n x_i^2 + n \bar{x}^2 - 2 n\bar{x}^2 \right] \\
&= - \bar{x}^2 + \frac{1}{n} \sum_{i=1}^n x_i^2 .
\end{align}](../w/images/math/e/0/6/e06e14af14e6327a485ca0dbeb903acd.png)
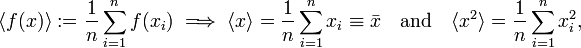
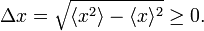
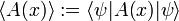
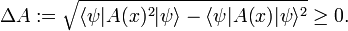
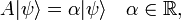
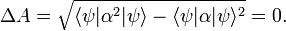
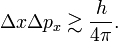
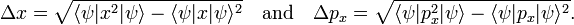
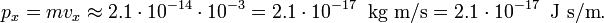
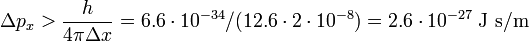
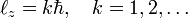
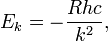
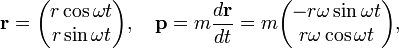
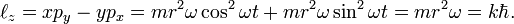
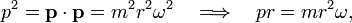
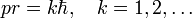
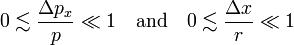
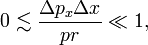
![\frac{\Delta p_x \Delta x}{p r}\gtrsim \frac{\hbar}{2pr} = \frac{1}{2 k }\quad \xrightarrow[k]{\text{large}} \quad 0,](../w/images/math/a/d/c/adcf68c4e6fb9d1e11ca5aa5744d0849.png)
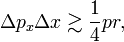
![\Delta A \Delta B \ge \frac{1}{2} \; \big\vert\langle\; [A,B]\; \rangle\big\vert
\quad \text{with}\quad [A,B] := AB - BA. \qquad\qquad\qquad\qquad \mathbf{(1)}](../w/images/math/5/0/6/506d94f0f110348c4ea6118476b0abe7.png)
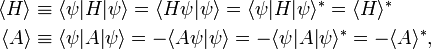
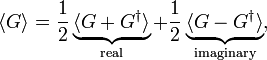
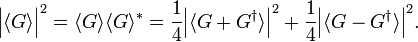
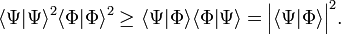

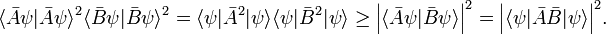

![\bar{A}\bar{B} - \bar{B}\bar{A} = [A,B]](../w/images/math/d/4/e/d4e6713484f6642870bb63af347faa2a.png)
![\langle \psi| \bar{A}^2| \psi \rangle \langle \psi| \bar{B}^2| \psi \rangle
\ge \frac{1}{4}
\Big\vert\langle \psi|\bar{A}\bar{B} + \bar{B}\bar{A}|\Psi\rangle \Big\vert^2
+
\frac{1}{4} \Big\vert\langle \psi|[A,B] |\psi\rangle \Big\vert^2.
\qquad\qquad\qquad\quad\mathbf{(2)}](../w/images/math/a/1/3/a13d1935c5208362c9046eea1acd660c.png)
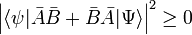
![\langle \psi| \bar{A}^2| \psi \rangle \langle \psi| \bar{B}^2| \psi \rangle
\ge
\frac{1}{4} \Big\vert\langle \psi|[A,B] |\psi\rangle \Big\vert^2.](../w/images/math/4/a/e/4aeecb3ff0dbefc8eecbcf3d288444ad.png)
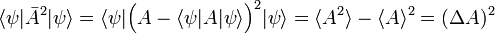
![(\Delta A \Delta B)^2 \ge \frac{1}{4} \Big\vert\langle \psi|[A,B] |\psi\rangle \Big\vert^2 ,](../w/images/math/5/a/4/5a4a774371473af5539f057121af672d.png)
![\begin{align}
&[L_z, L_+] = L_+, \quad L_z Y_{lm} = m Y_{lm}, \quad L_+Y_{lm} = c Y_{lm+1}, \\
&\langle Y_{lm} |[L_z,L_+] | Y_{lm}\rangle=\langle Y_{lm} |L_+ | Y_{lm}\rangle = c\langle Y_{lm} | Y_{lm+1}\rangle = 0.
\end{align}](../w/images/math/9/6/9/969e6ac5660d26014fe7a9656ab2ccc6.png)
![[p_x, x] = [ -i\hbar \frac{d}{dx}, x] = -i\hbar.](../w/images/math/6/d/d/6ddb96676e26d636d80b67b40fc6d362.png)
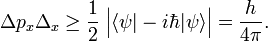
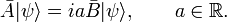
![\langle \psi| \bar{A}^2| \psi \rangle \langle \psi| \bar{B}^2| \psi \rangle
= \frac{1}{4}
\Big\vert\langle \psi|\bar{A}\bar{B} + \bar{B}\bar{A}|\Psi\rangle \Big\vert^2
+
\frac{1}{4} \Big\vert\langle \psi|[A,B] |\psi\rangle \Big\vert^2](../w/images/math/0/c/0/0c080c3bd2a9e95463a207a948aa4bf0.png)
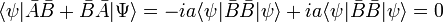
![\langle \psi| \bar{A}^2| \psi \rangle \langle \psi| \bar{B}^2| \psi \rangle
=
\frac{1}{4} \Big\vert\langle \psi|[A,B] |\psi\rangle \Big\vert^2.](../w/images/math/a/5/a/a5a2357c53f5bfb4f32dea3f7e2e4be0.png)
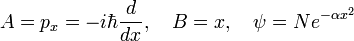
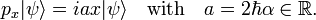
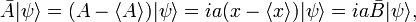
![\langle \psi| \bar{p_x}^2| \psi \rangle \langle \psi| \bar{x}^2| \psi \rangle
=
\frac{1}{4} \Big\vert\langle \psi|[p_x,x] |\psi\rangle \Big\vert^2.](../w/images/math/9/f/3/9f3542fe7c4fab8fd94bc9ffb878eb75.png)
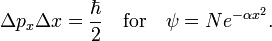
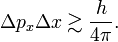
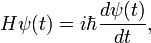
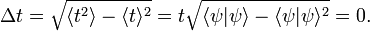
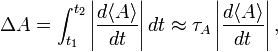
![\begin{align}
\frac{d \langle A \rangle}{dt} &=
\Big\langle \frac{d \psi(t) }{dt} | A | \psi(t) \Big\rangle + \Big\langle \psi(t)|A| \frac{d \psi(t) }{dt} \Big \rangle
=
\frac{1}{i\hbar}\Big( \langle - H \psi | A | \psi \rangle + \langle \psi|A H | \psi \rangle \Big) \\
&= \frac{1}{i\hbar} \langle \psi | [A, H] | \psi \rangle,
\end{align}](../w/images/math/f/7/2/f729759f13f85bc1e5f15259ee0c4428.png)
![\Big| \langle \psi | [A, H] | \psi \rangle \Big| = \hbar \left|\frac{d \langle A \rangle} {dt}\right|.](../w/images/math/8/1/e/81e826aed9795774638ea0b62859df4a.png)
![\frac{1}{2} \big\vert\langle\;\psi| [H,A] |\psi\; \rangle\big\vert \le \Delta E \Delta A,](../w/images/math/3/e/a/3eae397b782927854fea6bda97ccdb33.png)