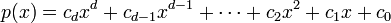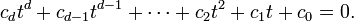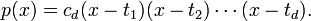Fundamental Theorem of Algebra

From Knowino

Jump to: navigation, search

The Fundamental Theorem of Algebra is a mathematical theorem stating that every nonconstant polynomial whose coefficients are complex numbers has at least one complex number as a root. In other words, given any polynomial

$p(x) = c_d x^d + c_{d-1} x^{d-1} + \cdots + c_2 x^2 + c_1 x + c_0$

(where $d$ is any positive integer), we can find a complex number $t$ so that

$c_d t^d + c_{d-1} t^{d-1} + \cdots + c_2 t^2 + c_1 t + c_0 = 0.$

One important case of the Fundamental Theorem of Algebra is that every nonconstant polynomial with real coefficients must have at least one complex root. Since it is not true that every such polynomial has to have at least one real root (as the example $p (x) = x 2 + 1$ demonstrates), many mathematicians feel that the complex numbers form the most natural setting for working with polynomials.

In fact, a stronger version of the Fundamental Theorem of Algebra is also true: a polynomial of degree $d$ can be factored completely into a product of $d$ linear polynomials:

$p(x) = c_d (x-t_1) (x-t_2) \cdots (x-t_d).$

A way of saying this is that every polynomial of degree $d$ has exactly $d$ complex roots, "counting multiplicity".

Carl Friedrich Gauss is generally credited with the first satisfactory proof of this theorem, his proof being the principal result in his Ph.D. thesis finished in 1799.

[edit] Proving the Fundamental Theorem of Algebra

[edit] Using complex analysis

A startlingly simple proof is based on Liouville's theorem: If $p (z)$ is a polynomial function of a complex variable then both $p (z)$ and $1 / p (z)$ will be holomorphic in any domain where $\scriptstyle p(z) \ne 0$ . But, by the triangle inequality, we know that outside a neighborhood of the origin $| p (z) | > | p (0) |$ , so if there is no $z 0$ such that $p (z 0) = 0$ , we know that $1 / p (z)$ is a bounded entire (i.e., holomorphic in all of $\mathbb{C}$ ) function. By Liouville's theorem, it must be constant, so $p (z)$ must also be constant.

[edit] Using algebra (and a bit of real analysis)

There are also proofs that do not depend on complex analysis, but they require more algebraic or topological machinery.

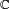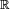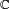We need to show that any algebraic extension of $\scriptstyle\mathbb{C}$ has degree one. Since $\scriptstyle\mathbb{C} = \mathbb{R}[i]$ , any such field extension also extends $\scriptstyle\mathbb{R}$ . 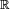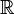Now, any $\scriptstyle\alpha$ algebraic over $\scriptstyle\mathbb{C}$ must also be algebraic over $\scriptstyle\mathbb{R}$ , but its minimal polynomial cannot be of odd degree, because any such polynomial must have a real root by the intermediate value theorem, so the splitting field of $\scriptstyle\alpha$ over $\mathbb{R}$ must have degree a power of 2. Its Galois group must have a normal subgroup of index 2, but a generating element must already be in 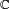$\scriptstyle\mathbb{C}$ by the quadratic formula. This shows that the extension has, at most, degree 2, but appealing once again to the quadratic formula, we see that $\scriptstyle\mathbb{C}$ is closed under quadratic extensions, so $\scriptstyle\mathbb{C}$ must itself be algebraically closed.

[edit] Using the fundamental group of the punctured plane 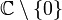$\mathbb{C}\setminus\{0\}$

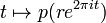We can assume without loss of generality that the leading coefficient of $p (z)$ is 1. Now assume that $p$ has no roots. Then, the maps $[0,1]\to\mathbb{C}\setminus\{0\}$ given by $t\mapsto p(r e^{2\pi i t})$ are homotopic in 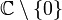$\mathbb{C}\setminus\{0\}$ for all $r$ , and hence they are all null homotopic there (take $r = 0$ ). 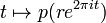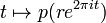However, for large enough $r$ , the maps $[0,1]\to\mathbb{C}\setminus\{0\}$ given by $t\mapsto p(r e^{2\pi i t})$ and $t\mapsto r^d e^{2d\pi i t}$ (where $d$ is the degree of the polynomial $p$ ) are homotopic, and thus $t\mapsto p(r e^{2\pi i t})$ is not null homotopic.

[edit] Using the second homotopy group of the Riemann sphere 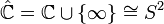$\hat{\mathbb{C}}=\mathbb{C}\cup\{\infty\}\cong S^2$

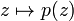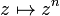Without loss of generality the leading coefficient of $p (z)$ is 1. We consider $z\mapsto p(z)$ as a map from the Riemann sphere to itself (taking infinity to infinity). By considering the homotopy $t z n + (1 - t) p (z)$ , where $t\in [0,1]$ , this map is homotopic to the map $z\mapsto z^n$ . Hence it suffices to show that the map 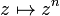$z\mapsto z^n$ is not null homotopic. 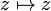However, in the homotopy group $π 2 (S 2)$ we have $[z\mapsto z^n] = [z\mapsto z][z\mapsto z^{n-1}]$ , and so it suffices to show that $z\mapsto z$ is not null homotpic, which is equivalent to the fact that the sphere is not contractible.