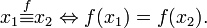Equivalence relation

From Knowino

Jump to: navigation, search

In mathematics, an equivalence relation is a (binary) relation between objects that formalises the intuitive notion that related objects have some specific property in common. Examples include equality between numbers or other quantities; geometrical relations such as parallel, congruence, similarity; abstract algebraic concepts such as isomorphism. The equivalence may be expressed by formulae, geometric concepts or algorithms, but in keeping with the modern definition of mathematics, it is most convenient to identify an equvialence relation with the sets of objects for which it holds true.

A relation 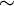$\sim\,$ on a set X is an equivalence relation if it satisfies the following three properties

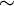$\sim\,$ is reflexive: 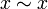$x \sim x\,$ for all $x \in X$ .
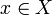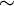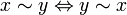$\sim\,$ is symmetric: $x\sim y \Leftrightarrow y \sim x$ .
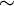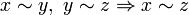$\sim\,$ is transitive: $x \sim y,~y\sim z \Rightarrow x \sim z$ .

An equivalence class for 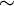$\sim\,$ is the set of elements of X all related to some particular element

$[x]_\sim = \{ y \in X : x \sim y \} . \,$

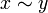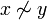The equivalence classes form a partition of the set X, that is, two classes $[x] \sim$ and $[y] \sim$ are either equal (have the same members), which is the case when $x \sim y\,$ , or are disjoint (have no members in common), which is the case when $x \not\sim y$ .

[edit] Examples

On any set X, the identity relation 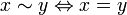$x \sim y \Leftrightarrow x = y$ . The equivalence classes are the singleton sets ${x}$ .
On any set X, the universal relation 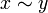$x \sim y\,$ for all x,y. There is one equivalence class, X itself.
On the integers, parity: 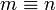$m \equiv n$ iff m,n have the same remainder on division by 2. There are two equivalence classes, "even" and "odd".
On the integers more generally, modular arithmetic operates on the equivalence classes defined by remainder on division by a fixed modulus M.
On lines in the plane, being parallel (or coincide). The equivalence classes are the directions.
On triangles in the plane, being congruent.
On triangles in the plane, being similar.

[edit] Quotient classes

It will be seen in the examples that a common way of defining an equivalence relation is to state that elements have some common property. We can formalise this by saying that if f is a function defined on the set X, we define the relation 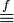$\stackrel{f}{\equiv}$ by

$x_1 \stackrel{f}{\equiv} x_2 \Leftrightarrow f(x_1) = f(x_2) . \,$

This is an equivalence relation, the kernel of f. Every equivalence relation can be defined in this way for a suitable function f.

Some content on this page may previously have appeared on Citizendium.

Equivalence relation

[edit] Examples

[edit] Quotient classes

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox