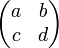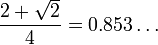Entanglement (physics)

There are three interrelated meanings of the word entanglement in physics. They are listed below and then discussed, both separately and in relation to each other.

• A combination of empirical facts, observed or only hypothetical, incompatible with the conjunction of three fundamental assumptions about nature, called "counterfactual definiteness", "relativistic local causality" and "no-conspiracy" (see below), but compatible with the conjunction of the last two of them ("relativistic local causality" and "no-conspiracy"). Such a combination will be called "empirical entanglement" (which is not a standard terminology^[1]).
• A prediction of the quantum theory stating that the empirical entanglement must occur in appropriate physical experiments (called "quantum entanglement").
• In quantum theory there is a technical notion of "entangled state".

Entanglement cannot be reduced to shared randomness, and does not imply faster-than-light communication.

Due to quantum entanglement, quantum information is different from classical information, which leads to quantum communication, quantum games, quantum cryptography and quantum computation.

Contents 1 Empirical entanglement 1.1 The framework, and local causality 1.2 Falsifiabilty, and no-conspiracy assumption 1.3 Counterfactual definiteness 1.4 Local causality and counterfactual definiteness 1.5 Example 1.6 Entanglement is not just shared randomness 2 Quantum entanglement 2.1 Classical bounds and quantum bounds 2.2 Experimental status 2.3 Communication channels 3 Entangled quantum states 4 Nonlocality and entanglement 4.1 In general 4.2 For quantum states 5 Notes

[edit] Empirical entanglement

Some people understand it easily, others find it difficult and confusing.

It is easy, since no physical or mathematical prerequisites are needed. Nothing like Newton laws, Schrödinger equation, conservation laws, nor even particles or waves. Nothing like differentiation or integration, nor even linear equations.

It is difficult and confusing for the very same reason! It is highly abstract. Many people feel uncomfortable in such a vacuum of concepts and rush to return to the particles and waves.

[edit] The framework, and local causality

The following concepts are essential here.

• A physical apparatus that has a switch and several lights. The switch can be set to one of several possible positions. A little after that the apparatus flashes one of its lights.
• "Local causality": widely separated apparatuses are incapable of signaling to each other.

Otherwise the apparatuses are not restricted; they may use all kinds of physical phenomena. In particular, they may receive any kind of information that reaches them. We treat each apparatus as a black box: the switch position is its input, the light flashed is its output; we need not ask about its internal structure.

However, not knowing what is inside the black boxes, can we know that they do not signal to each other? There are two approaches, non-relativistic ("loose") and relativistic ("strict").

The loose approach: we open the black boxes, look, see nothing like mobile phones and rely on our knowledge and intuition.

The strict approach: we do not open the black boxes. Rather, we place them, say, 360,000 km apart (the least Earth-Moon distance) and restrict the experiment to a time interval of, say, 1 sec. Relativity theory states that they cannot signal to each other, for a good reason: a faster-than-light communication in one inertial reference frame would be a backwards-in-time communication in another inertial reference frame!

Below, the strict approach is used (unless explicitly stated otherwise). Thus, the apparatuses are not restricted. They may contain mobile phones or whatever. They may interact with any external equipment, be it cell sites or whatever.

[edit] Falsifiabilty, and no-conspiracy assumption

A claim is called falsifiable (or refutable) if it has observable implications. If some of these implications contradict some observed facts then the claim is falsified (refuted). Otherwise it is corroborated.

The relativistic local causality was never falsified; that is, a faster-than-light signaling was never observed. Does it mean that local causality is corroborated? This question is more intricate than it may seem.

Let A, B be two widely separated apparatuses, x_A the input (the switch position) of A, and y_B the output (the light flashed) of B. (For now we do not need y_A and x_B.) Local causality claims that x_A has no influence on y_B.

An experiment consisting of n trials is described by x_A(i), y_B(i) for i = 1,2,...,n. Imagine that n = 4 and

x_A(1) = 1,   x_A(2) = 2,   x_A(3) = 1,   x_A(4) = 2,  

y_B(1) = 1,   y_B(2) = 2,   y_B(3) = 1,   y_B(4) = 2.

The data suggest that x_A influences y_B, but do not prove it. Two alternative explanations are possible:

• the apparatus B chooses y_B at random (say, tossing a coin); the four observed equalities y_B(i) = x_A(i) are just a coincidence (of probability 1/16);
• the apparatus B alternates 1 and 2, that is, y_B(i) = 1 for all odd i but y_B(i) = 2 for all even i.

Consider a more thorough experiment: n = 1000, and x_A(i) are chosen at random, say, tossing a coin. Imagine that y_B(i) = x_A(i) for all i = 1,2,...,n. The influence of x_A on y_B is shown very convincingly! But still, an alternative explanation is possible.

For choosing x_A, the coin must be tossed within the time interval scheduled for the trial, since otherwise a slower-than-light signal can transmit the result to the apparatus B before the end of the trial. However, is the result really unpredictable in principle (not just in practice)? Not necessarily so. Moreover, according to classical mechanics, the future is uniquely determined by the past! In particular, the result of the coin tossing exists in the past as a complicated function of a huge number of coordinates and momenta of micro particles.

It is logically possible, but quite unbelievable that the future result of coin tossing is somehow spontaneously singled out in the microscopic chaos and transmitted to the apparatus B in order to influence y_B. The no-conspiracy assumption claims that such exotic scenarios may be safely neglected.

The conjunction of the two assumptions, relativistic local causality and no-conspiracy, is falsifiable, but was never falsified; thus, both assumptions are corroborated.

Below, the no-conspiracy is always assumed (unless explicitly stated otherwise).

[edit] Counterfactual definiteness

In this section a single apparatus is considered.

A trial is described by a pair (x,y) where x is the input (the switch position) and y is the output (the light flashed). Is y a function of x? We may repeat the trial with the same x and get a different y (especially if the apparatus tosses a coin). We can set the switch to x again, but we cannot set all molecules to the same microstate. Still, we may try to imagine the past changed, asking a counterfactual question:^[2]

• Which outcome the experimenter would have received (in the same trial) if he/she did set the switch to another position?

It is meant that only the input x is changed in the past, nothing else. The question may seem futile, since an answer cannot be verified empirically. Strangely enough, the question will appear to be very useful in the next section.

Classical physics can interpret the question as a change of external forces acting on a mechanical system of a large number of microscopic particles. It is unfeasible to calculate the answer, but anyway, the question makes sense, and the answer exists in principle:

y = f(x)

for some function f : X → Y, where X is the finite set of all possible inputs, and Y is the finite set of all possible outputs. Existence of this function f is called "counterfactual definiteness".

Repeating the experiment we get

y(i) = f_i(x(i))

for i = 1,2,... Each time a new function f_i appears; thus x(i)=x(j) does not imply y(i)=y(j). In the case of a single apparatus, counterfactual definiteness is not falsifiable, that is, has no observable implications. Surprisingly, for two (and more) apparatuses the situation changes dramatically.

[edit] Local causality and counterfactual definiteness

For two apparatuses, A and B, an experiment is described by two pairs, (x_A,y_A) and (x_B,y_B) or, equivalently, by a combined pair ((x_A,x_B), (y_A,y_B)). Counterfactual definiteness alone (without local causality) takes the form

(y_A,y_B) = f_A,B(x_A,x_B)

or, equivalently,

y_A = f_A(x_A,x_B),   y_B = f_B(x_A,x_B).

Assume in addition that A and B are widely separated and the local causality applies. Then x_A cannot influence y_B, and x_B cannot influence y_A, therefore

y_A = f_A(x_A),   y_B = f_B(x_B).

These f_A, f_B are one-time functions; another trial may involve different functions.

An alternative language is logically equivalent, but makes the presentation more vivid. Imagine an experimenter, Alice, near the apparatus A, and another experimenter, Bob, near the apparatus B. Alice is given some input x_A and must provide an output y_A. The same holds for Bob, x_B and y_B. Once the inputs are received, no communication is permitted between Alice and Bob until the outputs are provided. The input x_A is an element of a prescribed finite set X_A (not necessarily a number); the same holds for y_A and Y_A, x_B and X_B, y_B and Y_B.

It may seem that the apparatuses A, B are of no use for Alice and Bob. Significantly, this is an illusion.

[edit] Example

The simplest example of empirical entanglement is presented here. First, its idea is explained informally.

Alice and Bob pretend that they know a 2×2 matrix

consisting of numbers 0 and 1 only, satisfying four conditions:

a = b,   c = d,   a = c,   but   b ≠ d.

Surely they lie; these four conditions are evidently incompatible. Nevertheless Alice commits herself to show on request any row of the matrix, and Bob commits himself to show on request any column. We expect the lie to manifest itself on the intersection of the row and the column (not always but sometimes). However, Alice and Bob promise to always agree on the intersection!

More formally, x_A=1 requests from Alice the first row, x_A=2 the second; in every case y_A must be eithe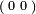r or 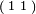. From Bob, x_B=1 requests the first column, in which case y_B must be 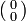or 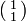; and x_B=2 requests the second column, in which case y_B must be 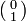or 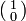. The agreement on the intersection means that, for example, if x_A=2 and x_B=1 then the first element of the row y_A must be equal to the second element of the column y_B.

Without special apparatuses (A and B), Alice and Bob surely cannot fulfill their promise. Can the apparatuses help? This crucial question is postponed to the section "Quantum entanglement". Here we consider a different question: is it logically possible, under given assumptions, that Alice and Bob fulfill their promise?

Under all the three assumptions (counterfactual definiteness, local causality and no-conspiracy) we have y_A = f_A(x_A) and y_B = f_B(x_B) for some functions f_A, f_B. (These functions may change from one trial to another.) Specifically, f_A(1) and f_A(2), being two rows, form a 2×2 matrix satisfying the conditions a=b, c=d. Also f_B(1) and f_B(2), being two columns, form a 2×2 matrix satisfying the conditions a=c, b≠d. These two matrices necessarily differ at least in one of the four elements (since the four conditions are incompatible). Therefore it can happen that Alice and Bob disagree on the intersection, and moreover, it happens with the probability at least 0.25. In the long run, Alice and Bob cannot fulfill their promise.

Waiving the counterfactual definiteness (but retaining local causality and no-conspiracy) we get the opposite result: Alice and Bob can fulfill their promise. Here is how.

Given x_A and x_B, there are two allowed y_A and two allowed y_B, thus, 4 allowed combinations (y_A, y_B). Two of them agree on the intersection of the row and the column; the other two disagree. Imagine that the apparatuses A, B choose at random (with equal probabilities 0.5, 0.5) one of the two combinations (y_A, y_B) that agree on the intersection. For example, given x_A=2 and x_B=1, we get either y_A = 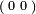and y_B = 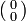, or y_A = 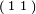and y_B = .

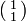This situation is compatible with local causality, since y_B gives no information about x_A; also y_A gives no information about x_B. For example, given x_A=2 and x_B=1, we get either y_B = 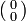or y_B = 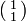, with probabilities 0.5, 0.5; exactly the same holds given x_A=1 and x_B=1.

Thus, empirical entanglement is logically possible. The question of its existence in the nature is addressed in the section "Quantum entanglement".

[edit] Entanglement is not just shared randomness

Widely separated apparatuses, unable to signal to each other, can be correlated. Correlations are established routinely by communication. For example, Alice and Bob, reading their copies of a newspaper, learn the result of yesterday's lottery drawing. This is called shared randomness. Likewise, the apparatuses A, B can share randomness by receiving signals from some external common source. However, shared randomness obeys the three assumptions (counterfactual definiteness, local causality and no-conspiracy) and therefore cannot produce entanglement. In other words, entanglement as a resource is substantially stronger than shared randomness.

[edit] Quantum entanglement

[edit] Classical bounds and quantum bounds

Classical physics obeys the counterfactual definiteness and therefore negates entanglement. Classical apparatuses A, B cannot help Alice and Bob to always win (that is, agree on the intersection). What about quantum apparatuses? The answer is quite unexpected.

First, quantum apparatuses cannot ensure that Alice and Bob win always. Moreover, the winning probability does not exceed

no matter which quantum apparatuses are used.

Second, there exist quantum apparatuses that ensure a winning probability higher than 3/4 = 0.75. This is a manifestation of entanglement, since under the three classical assumptions (counterfactual definiteness, local causality and no-conspiracy) the winning probability cannot exceed 3/4 (the classical bound). But moreover, ideal quantum apparatuses can reach the winning probability 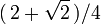(the quantum bound), and non-ideal quantum apparatuses can get arbitrarily close to this bound.

Third, a modification of the game, called "magic square game", makes it possible to win always. To this end we replace 2×2 matrices with 3×3 matrices, still of numbers 0 and 1 only, with the following conditions:

• the parity of each row is even,
• the parity of each column is odd.

The classical bound is equal to 8/9; the quantum bound is equal to 1.

[edit] Experimental status

Many amazing entanglement-related predictions of the quantum theory were tested in ingenious experiments using high-tech equipment. All tested predictions are confirmed. Still, each one of these experiments has a "loophole", that is, admits alternative, entanglement-free explanations. Such explanations are highly contrived. They would be rejected as unbelievable in a routine development of science. However, the entanglement problem is exceptional: fundamental properties of nature are at stake! Entanglement is also unbelievable for many people. Thus, the problem is still open; finer experiments will follow, until an unambiguous result will be achieved.

[edit] Communication channels

According to the quantum theory, quantum objects manifest themselves via their influence on classical objects (more exactly, on classically described degrees of freedom). Every object admits a quantum description, but some objects may be described classically for all practical purposes, since their thermal fluctuations hide their quantal properties. These are called classical objects. Macroscopic bodies (more exactly, their coordinates) under usual conditions are classical. Digital information in computers is also classical.

A communication channel may be thought of as a chain of physical objects and physical interactions between adjacent objects. If all objects in the chain are quantal, the channel is called quantal. If at least one object in the chain is classical, the channel is called classical.

For example, newspapers, television, mobile phones and the Internet implement only classical channels. Quantum channels are usually implemented by sending a particle (photon, electron) or another microscopic object (ion) from a nonclassical source to a nonclassical detector through a low-noise medium.

Classical communication (that is, communication through a classical channel) can create shared randomness, but cannot create entanglement. Moreover, entanglement creation is impossible when Alice's apparatus A is connected to a source S by a quantum channel but Bob's apparatus B is connected to S by a classical channel. Here is an explanation.

The classical channel S-B is a chain containing a classical object C. By assumption, no chain of interactions connects A and B (via S, or otherwise) bypassing C. Therefore A and B are conditionally independent given a possible state c of C. The response y_A of A to x_A given c need not be a function g_A(c,x_A) of c and x_A (uniqueness is not guaranteed), but still, we may choose one of possible responses y_A and let g_A(c,x_A) = y_A (so-called uniformization). Similarly, g_B(c,x_B) = y_B. Now, given c, the two one-time functions f_A(x_A) = g_A(c,x_A) and f_B(x_B) = g_B(c,x_B) lead to a possible disagreement of Alice and Bob (on the intersection of the row and the column) by the argument used before (in the section "Example"). A more thorough analysis shows that the classical bound on the winning probability, deduced before from the counterfactual definiteness, holds also in the case treated here.

[edit] Entangled quantum states

A bipartite or multipartite quantum state, pure or mixed, is called entangled, if it cannot be prepared by means of shared randomness and local quantum operations. A quantum state that can be used for violating classical bounds, that is, for producing empirical entanglement, is necessarily entangled. It is unclear whether the converse implication holds, or not. Some entangled mixed states, so-called Werner states, obey classical bounds for all one-stage experiments. But multi-stage experiments in general are still far from being well understood.

[edit] Nonlocality and entanglement

[edit] In general

The words "nonlocal" and "nonlocality" occur frequently in the literature on entanglement, which creates a lot of confusion: it seems that entanglement means nonlocality! This situation has two causes, pragmatical and philosophical.

Here is the pragmatical cause. The word "nonlocal" sounds good. The phrase "non-CFD" (where CFD denotes counterfactual definiteness) sounds much worse, but is also incorrect; the correct phrase, involving both CFD and locality (and no-conspiracy, see the lead) is prohibitively cumbersome. Thus, "nonlocal" is often used as a conventional substitute for "able to produce empirical entanglement".^[3]

The philosophical cause. Many people feel that CFD is more trustworthy than RLC (relativistic local causality), and NC (no-conspiracy) is even more trustworthy. Being forced to abandon one of them, these people are inclined to retain NC and CFD at the expence of abandoning RLC.

However, the quantum theory is compatible with RLC+NC. A violation of RLC+NC is called faster-than-light communication (rather than entanglement); it was never observed, and never predicted by the quantum theory. Thus RLC and NC are corroborated, while CFD is not. In this sense CFD is less trustworthy than RLC and NC.

[edit] For quantum states

Quantitative measures for entanglement are scantily explored in general. However, for pure bipartite quantum states the amount of entanglement is usually measured by the so-called entropy of entanglement. On the other hand, several natural measures of nonlocality are invented (see above about the meaning of "nonlocality"). Strangely enough, non-maximally entangled states appear to be more nonlocal than maximally entangled states, which is known as "anomaly of nonlocality"; nonlocality and entanglement are not only different concepts, but are really quantitatively different resources.^[4] According to the asymptotic theory of Bell inequalities, even though entanglement is necessary to obtain violation of Bell inequalities, the entropy of entanglement is essentially irrelevant in obtaining large violation.^[5]

[edit] Notes

1. ↑ Experts often call it "nonlocality", thus confusing non-experts; see Sect. 4.1.
2. ↑ "Die Geschichte kennt kein Wenn" (Karl Hampe). Whether physics has subjunctive mood or not, this is the question of counterfactual definiteness.
3. ↑ Physical terminology can mislead non-experts. Some examples: "quantum telepathy"; "quantum teleportation"; "Schrödinger cat state"; "charmed particle".
4. ↑ A.A. Methot and V. Scarani, "An anomaly of non-locality" (2007), Quantum Information and Computation, 7:1/2, 157-170; also arXiv:quant-ph/0601210.
5. ↑ M. Junge and C. Palazuelos, "Large violation of Bell inequalities with low entanglement" (2010), arXiv:1007.3043.