Continuity equivalence theorem

From Knowino

Pending changes are displayed on this page

Unchecked

Jump to: navigation, search

[edit] Theorem

Let $X$ and $Y$ be two non-empty topological spaces, and 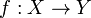$f:X\to Y$ a function from $X$ to $Y$ . Then the following are equivalent:

$f$ is continous;
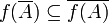For all subset $A$ of $X$ we have $f(\overline A)\subseteq \overline {f(A)}$ ;
The inverse image of a closed set in $Y$ is closed in $X$ ;
The inverse image of an open set in $Y$ is open in $X$ .

[edit] Proof

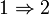
$1\Rightarrow 2$

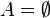
The inclusion holds if $A=\emptyset$
Let 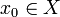$x_0\in X$ be an adherent point for $A$
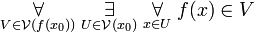$\underset{V\in \mathcal V(f(x_0))}{\forall} \; \underset{U\in \mathcal V(x_0)}{\exists} \; \underset{x\in U}{\forall} \; f(x)\in V$ (by continuity)
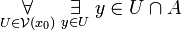$\underset{U\in \mathcal V(x_0)}{\forall} \; \underset{y\in U}{\exists} \; y\in U\cap A$ (by definition)
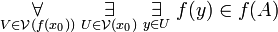$\underset{V\in \mathcal V(f(x_0))}{\forall} \; \underset{U\in \mathcal V(x_0)}{\exists}\; \underset{y\in U}{\exists} \; f(y)\in f(A)$ (by 3 and 4)
$f (x 0)$ is an adherent point for $f (A)$ (by definition)

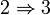
$2\Rightarrow 3$

Let $G$ be a closed set in $Y$
Define $F = f - 1 (G)$
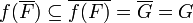$f(\overline F)\subseteq \overline{f(F)}=\overline G=G$ (by hypothesis and definition)
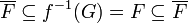$\overline F\subseteq f^{-1}(G)=F\subseteq \overline F$ (by 2, 3, definition and definition)
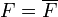$F=\overline F$ and therefore is closed (by 4)

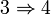
$3\Rightarrow 4$

Let $V$ be open in $Y$ and $U = f - 1 (V)$
$U c = (f - 1 (V)) c = f - 1 (V c)$ (by definition of inverse image and complement)
$V c$ is closed (by definition)
$f - 1 (V c)$ is closed (by hypothesis)
$U$ is open (by definition)

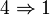
$4\Rightarrow 1$

Let 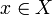$x\in X$ , and $V$ be a neighbourhood of $f (x)$
$U = f - 1 (V)$ is open in $X$ (by hypothesis)
$U$ is a neighbourhood of $x$ (by definition and definition)
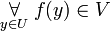$\underset{y\in U}{\forall} \; f(y)\in V$ (by definition)
$f$ is continuous (by definition)

[edit] Notations used

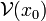$\mathcal V(x_0)$ : the set of neighbourhoods of $x 0$
$f - 1 (G)$ : the inverse image of $G$ by $f$
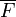$\overline F$ : the closure of $F$
$U c$ : the complement of $U$

Some content on this page may previously have appeared on Bourbawiki.

Retrieved from "http://knowino.org/wiki/Continuity_equivalence_theorem"

Category: Topology Theorems

Personal tools

Log in / create account

Community

Toolbox