Compactness axioms

In general topology, the important property of compactness has a number of related properties.

The definitions require some preliminary terminology. A cover of a set X is a family 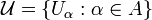such that the union 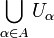is equal to X. A subcover is a subfamily which is again a cover 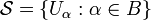where B is a subset of A. A refinement is a cover 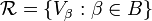such that for each β in B there is an α in A such that . A cover is finite or countable if the index set is finite or countable. A cover is point finite if each element of X belongs to a finite numbers of sets in the cover. The phrase "open cover" is often used to denote "cover by open sets".

[edit] Definitions

We say that a topological space X is

• Compact if every cover by open sets has a finite subcover.
• A compactum if it is a compact metric space.
• Countably compact if every countable cover by open sets has a finite subcover.
• Lindelöf if every cover by open sets has a countable subcover.
• Sequentially compact if every convergent sequence has a convergent subsequence.
• Paracompact if every cover by open sets has an open locally finite refinement.
• Metacompact if every cover by open sets has a point finite open refinement.
• Orthocompact if every cover by open sets has an interior preserving open refinement.
• σ-compact if it is the union of countably many compact subspaces.
• Locally compact if every point has a compact neighbourhood.
• Strongly locally compact if every point has a neighbourhood with compact closure.
• σ-locally compact if it is both σ-compact and locally compact.
• Pseudocompact if every continuous real-valued function is bounded.

Some content on this page may previously have appeared on Citizendium.