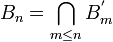Basic properties of closed sets
[edit] Theorem
Let X be a topological space and A a subset of X. Then
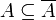
- If (xn) is a convergent sequence of points in A, its limit is an element of
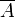 .
.
- If X satifies the first countability axiom and
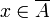 , then there exists a convergent sequence (xn) of points in A such that
, then there exists a convergent sequence (xn) of points in A such that 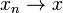 .
.
[edit] Proof
1. The definition of adherent point implies immediately that all points of A are adherent points for A.
2. Let (xn) be a convergent sequence of points in A and x its limit, and let 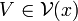 . By definition of limit there exists
. By definition of limit there exists 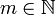 such that for all n > m,
such that for all n > m, 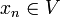 . But, by hypothesis, for all n > m,
. But, by hypothesis, for all n > m, 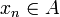 , hence
, hence 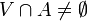 , meaning that x is an adherent point for A.
, meaning that x is an adherent point for A.
3. Let 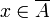 and consider a countable fundamental system of neighbourhoods of x,
and consider a countable fundamental system of neighbourhoods of x, 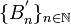 (which exists by definition). Construct a chain (ordered by inclusion)
(which exists by definition). Construct a chain (ordered by inclusion) 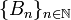 by setting
by setting
for all 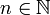 . Note that this chain is still a fundamental system. Now for each n, let
. Note that this chain is still a fundamental system. Now for each n, let 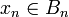 . Let us prove that
. Let us prove that 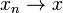 . Suppose
. Suppose 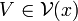 . Then (by definition) there exists
. Then (by definition) there exists 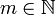 such that
such that 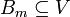 . But since
. But since 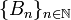 is a chain, we have
is a chain, we have
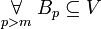 ,
,
and hence
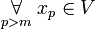 which ends the proof.
which ends the proof.
| |
Some content on this page may previously have appeared on Bourbawiki. |