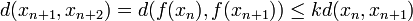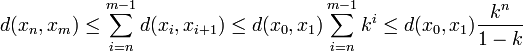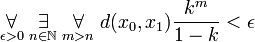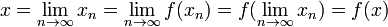Banach fixed point theorem
[edit] Theorem
Let (M,d) be a complete metric space and f a contraction on M with Lipschitz constant k. Then there exists a unique 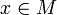 such that f(x) = x.
such that f(x) = x.
[edit] Proof
Let us define a sequence (xn) of elements in M in the following way
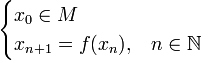 ,
,
and show that this sequence is a Cauchy sequence.
Since f is a contraction, we have that, for 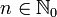
which results in the formula
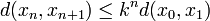 , for any
, for any 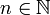 .
.
As such, we obtain, for any 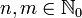 (
(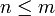 )
)
by basic results on geometric series.
Since 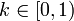 ,
, 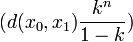 is a sequence converging to 0, and hence
is a sequence converging to 0, and hence
which results in
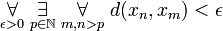 ,
,
or, in other words, (xn) is a Cauchy sequence.
M being complete, (xn) converges to a point which we will call x.
Finally, since f is a contraction, it is continuous, and hence, the following holds
which states that x is a fixed point of f.
To prove uniqueness, suppose y 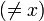 is also a fixed point of f. Then
is also a fixed point of f. Then
- d(x,y) > 0,
and we would also obtain
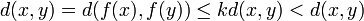 ,
,
resulting in a contradiction.
| |
Some content on this page may previously have appeared on Bourbawiki. |