Statistical/Machine Learning
Semester 1 2024-2025
Thursday 17-20, Schreiber 006
Announcements and Handouts
7 November:
Notes for class 1
Some data examples slides
r code for class 1
14 November:
Notes for class 2
Homework 1 (due 28 November before class). Submission in pairs is possible, but not in triplets or more
please.
Competition instructions are now available. Some code to read and examine the training data.
21 November:
Notes for class 3
Slides demonstrating the bias-variance decomposition in Fixed-X linear regression from a geometric
perspective
28 November:
Notes for class 4
Homework 2(you may find this writeup on quantile regression helpful).
5 December:
Notes for class 5
Code for running regularized regression and PCA on competition data.
5 December:
We will discuss Lasso from last week’s note, then as time allows start discussion classification, from this
note for class 6
Code for running classification methods on competition data.
19 December:
Note for class 7
Code for running classification methods on competition data.
22 December:
Homework 3, due on 7 January.
26 December:
Note for class 8
Code for running trees (and random forest) on competition data.
3 January:
Note for class 9
10 January:
Note for class 10
Code for running gradient boosting on competition data.
16 January:
Note for class 11
17 January:
Full Homework 4, due date extended to 27 January.
Note: The two practice finals will be handed out after the class on 23/1, and will be solved in class on
30/1. You should leave time in the last week to work on them so it is recommended to submit HW4 as
early as possible.
23 January:
Note for class 12
First practice exam (partially based on homework problems)
27 January:
Second practice exam — please try to solve before class
28 January:
Competition final results: 16 submissions, 12 in the bonus, the winner is team RMSE Fighter (Atir
Nafshi) with a score of 0.75103.
Syllabus
The goal of this course is to gain familiarity with the basic ideas and methodologies of statistical
(machine) learning. The focus is on supervised learning and predictive modeling, i.e., fitting y ≈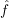 (x), in
regression and classification.
(x), in
regression and classification.
We will start by thinking about some of the simpler, but still highly effective methods, like nearest
neighbors and linear regression, and gradually learn about more complex and “modern” methods and
their close relationships with the simpler ones.
As time permits, we will also cover one or more industrial “case studies” where we track the process from
problem definition, through development of appropriate methodology and its implementation, to
deployment of the solution and examination of its success in practice.
The homework and exam will combine hands-on programming and modeling with theoretical analysis.
Topics list:
-
Introduction (text chap. 1,2): Local vs. global modeling; Overview of statistical considerations:
Curse of dimensionality, bias-variance tradeoff; Selection of loss functions; Basis expansions
and kernels
-
Linear methods for regression and their extensions (text chap. 3): Regularization, shrinkage
and principal components regression; Quantile regression
-
Linear methods for classification (text chap. 4): Linear discriminant analysis; Logistic
regression; Linear support vector machines (SVM)
-
Classification and regression trees (text chap. 9.2)
-
Model assessment and selection (text chap. 7): Bias-variance decomposition; In-sample error
estimates, including Cp and BIC; Cross validation; Bootstrap methods
-
Basis expansions, regularization and kernel methods (text chap. 5,6): Splines and polynomials;
Reproducing kernel Hilbert spaces and non-linear SVM
-
Committee methods in embedded spaces (material from chaps 8-10): Bagging, random forest
and boosting
-
Segue into “Statistical Learning Theory” basics in the ML literature and comparison between
approaches for analysis and model selection
-
Deep learning and its relation to statistical learning
-
Case studies: Customer wallet estimation; Netflix prize competition; maybe others...
Prerequisites
Basic knowledge of mathematical foundations: Calculus; Linear Algebra; Geometry
Undergraduate courses in: Probability; Theoretical Statistics
Statistical programming experience in R is not a prerequisite, but an advantage
Books and resources
Textbook:
Elements of Statistical Learning by Hastie, Tibshirani & Friedman
Book home page (including downloadable PDF of the book, data and errata)
Other recommended books:
Computer Age Statistical Inference by Efron and Hastie
Modern Applied Statistics with Splus by Venables and Ripley
Neural Networks for Pattern Recognition by Bishop
(Several other books on Pattern Recognition contain similar material)
All of Statistics and All of Nonparametric Statistics by Wasserman
Online Resources:
Data Mining and Statistics by Jerry Friedman
Statistical Modeling: The Two Cultures by the late, great Leo Breiman
Course on Machine Learning from Stanford’s Coursera.
The Netflix Prize competition is now over, but will still play a substantial role in our course.
Grading
There will be about four homework assignments, which will count for about 30% of the final grade, and a
final exam.
We will also have an optional data modeling competition, whose winners will get a boost in grade and
present to the whole class.
Computing
The course will require extensive use of statistical modeling software. It is recommended to use R
(freely available for PC/Unix/Mac), although this is not required, in particular Python is fine
too.
R Project website also contains extensive documentation.
Modern Applied Statistics with Splus by Venables and Ripley is an excellent source for statistical
computing help for R/Splus.
Using Python is also possible, the main downside is that the code I hand out (which in many cases is also
useful for the homework) is in R.
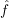 (x), in
regression and classification.
(x), in
regression and classification.