יחידה 9: ציוני תקן וההתפלגות הנורמלית  >> 9.4: דוגמאות

דוגמאות

להלן מספר דוגמאות המדגימות את חשיבות ואת תכונות ציוני התקן.

שאלה:

ידוע שציוני IQ מתפלגים נורמלית באוכלוסייה עם .

מהו אחוזון ה-IQ של יניב, אם ידוע שציון ה-IQ שלו 512?

פתרון:

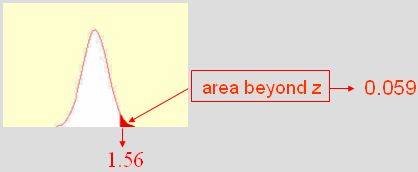
האחוזון הוא המשלים ל-1 של עמודה C ומציין את אחוז המקרים מתחת לערך זה ובמקרה זה הוא שווה

או לחילופין הסכום של עמודה B + 0.5 = 0.5+0.4406=0.9406.

ב-EXCEL הפקודה NORMSDIST(z) מחזירה את אחוזון הערך בהתפלגות הנורמלית, או במילים אחרות את אחוז הערכים עד אליו (עמודה B בטבלה + 0.5 של הערכים השליליים):

אחוזון: =NORMSDIST(1.56)=0.9406

בכדי לחשב מהו אחוז המקרים מעבר לערך (עמודה C) בטבלה יש להחסיר את תוצאת ה-NORMSDIST מ-1:           p=1-NORMSDIST(1.56)

שאלה:

המחלקה לפסיכולוגיה באוניברסיטה מסוימת מעוניינת לקבל סטודנטים מבין ה-20% הטובים ביותר במבחן הפסיכומטרי. מהו ציון הפסיכומטרי המינימלי לקבלה, אם ידוע ש- ?

פתרון:

אחוזון 80

מחפשים בטבלה בעמודה C את ציון התקן שמעבר אליו נופלים 20% מהמקרים - במקרה זה הערך הקרוב ביותר הוא ציון תקן z=0.84.

EXCEL:

הפקודה ב-EXCEL  לצורך מציאת ציון התקן המתאים לאחוזון מסוים היא NORMSINV, זוהי הפקודה ההפוכה ל-NORMSDIST ואליה יש להזין את האחוזון לו רוצים למצוא את ציון התקן:

=NORMSINV(percentile)

ובמקרה זה: =NORMSINV(0.8)=0.8416

ב-EXCEL ישנו דיוק גבוה יותר ולא רק עד שני מקומות לאחר הנקודה.

לאחר שמצאנו את ציון התקן יש להפוך אותו בחזרה לציוניים גולמיים. הפעם עלינו להציב את ציון ה-z לצורך מציאת ה-x.

584 הוא ציון הקבלה המינימלי (האחוזון ה-80).

שאלה:

מה היה ציון הפסיכומטרי המינימלי לקבלה, אם האחוזון המינימלי המבוקש היה 30?

פתרון:

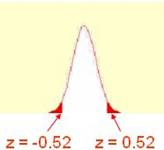
יש לשים לב שכאשר אנו מסתכלים על האזור התחתון של ההתפלגות, ערכי ה-z הם שליליים, ולא מופיעים בטבלה אבל כאמור מאחר וההתפלגות היא סימטרית, ניתן להסתכל על ערך ה-z המקביל באזור החיובי. השטח שמתחת ל:  -z זהה לשטח שמעל z.

לכן אם מבקשים את האחוזון ה-30 יש לחפש בעמודה C את הערך הקרוב ביותר ל-0.3. 

במקרה זה z=-0.52

ב-EXCEL אם נציב =NORMSINV(0.3)   נקבל ישירות ערך שלילי  =NORMSINV(0.3)=-0.5244

עכשיו יש להפוך את ציון ה-z לציון גולמי כפי שעשינו בדוגמא הקודמת:

שאלה:

עדי קיבל 410 בפסיכומטרי. איזה אחוז מהנבחנים קיבל ציון גבוה ממנו?

פתרון:

עתה יש לחשב את ציון התקן המתאים לציון הגולמי:

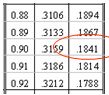
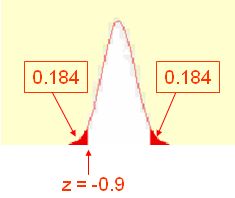
מצאנו שלפי עמודה C בטבלה יש מעבר אליו 18.41% מהציונים, אך מכיוון שזהו ציון תקן שלילי בעצם מתחתיו יש 18.41% מהמקרים. ובתרשים שלהלן זהו הזנב השמאלי.

לכן אחוז הנבחנים שקיבל ציון גבוה ממנו הוא:

ב-EXCEL ניתן או להזין NORMSDIST(-0.9) ולקבל את אחוז הערכים מתחת לציון התקן ואז להחסיר את התוצאה מ-1 כפי שעשינו בשימוש בעמודה C בטבלה.

לחילופין ניתן להזין את ציון התקן המקביל החיובי: z=0.9 ואז הפקודה תחשב את אחוז הערכים עד אליו: =NORMSDIST(0.9)=.816

שאלה:

מהו אחוז האנשים אשר יקבלו ציון פסיכומטרי בין 450 לבין 600?

פתרון:

לשאלה זו אין תשובה ישירה בטבלה או ב-EXCEL ולכן נצטרך לחשב את אחוז המקרים בין כל אחד מהערכים לממוצע ולסכום את שני המרחקים.

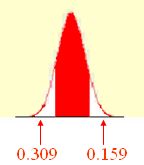
נחשב תחילה את ציון התקן המתאים ל-450:  .

הערך בעמודה C המתאים ל-z=0.5 הוא  ולכן זהו אחוז המקרים בין z=-0.5 לקצה השלילי של ההתפלגות.

עתה נחשב את ציון התקן המתאים ל-600:  .

מציון תקן 1 והלאה עד לסוף ההתפלגות יש 0.159 מהמקרים.

עתה בכדי לחשב את אחוז המקרים בין 450 ל-600 נחסיר את שני הזנבות הלא רצויים מ-1 ונחשב את אחוז המקרים בין 450 ל-600:   .

ניתן כמובן לבצע חישובי שטחים אחרים ולהשתמש בעמודה B בטבלה בכדי להגיע לתוצאה הרצויה. נסו זאת בעצמכם....

► חזור                    המשך ◄