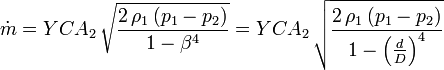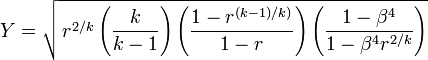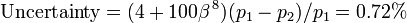Venturi tube

Author: Milton Beychok, March 17, 2010
A Venturi tube (or simply a venturi) is a section of piping consisting of an inlet converging conical section leading to a small diameter cylindrical section called the throat, followed by a diverging conical section leading to a cylindrical exit (see the adjacent drawing). A venturi gives a pressure differential that can be used to measure fluid (gas or liquid) flow rates, but it has countless other applications. For instance, in an automobile carburetor air runs through a venturi tube before it is mixed with gasoline vapor.
The volumetric flow rate, Q (unit volume per unit time, in SI units m3/s), of a fluid flowing through the venturi at any given point is the product of the cross-sectional area, A (SI unit: m2) at that point multiplied by the fluid's linear velocity, v (m/s), at that point. Since the volumetric flow rate is the same at any point within the venturi, the linear velocity of the fluid traveling through the smaller diameter throat of the venturi must increase which results in a decrease of pressure due to the conservation of energy, one of the conservation laws.
The gain in kinetic energy resulting from the increased linear velocity in the throat is offset (i.e., balanced) by the decrease of pressure in the throat. The reduction in pressure which occurs when the fluid flows through the throat is called the Venturi effect and is named after the Italian physicist Giovanni Battista Venturi (1746 - 1822) who first observed the effect.
Thus, referring to the adjacent drawing, the pressure p2 and the cross-sectional area A2 in the throat are smaller than the pressure p1 and the cross-sectional area A1 in the cylindrical inlet section. The linear velocity v2 in the throat is higher than the linear velocity v1 in the inlet section.
A venturi tube may also consist of non-cylindrical ducting rather than piping.
Contents |
[edit] Measuring fluid flow rate with a venturi
[edit] Incompressible fluid
Venturi tubes are used to accurately measure the volumetric flow of an ideal fluid, meaning that the fluid satisfies these conditions:[2][3]
- The fluid is nonviscous: There is no internal friction between layers of the fluid.
- The fluid is incompressible: The density of the fluid is constant (as is the case with liquids)
- The fluid flows without any turbulence: No element of the fluid has any angular velocity about its center, so there are no eddy currents present.
- The fluid flow is steady: The velocity, density and pressure at each point in the fluid does not change with time.
To obtain the volumetric flow rate of an incompressible fluid through a venturi, we start with this common form of the Bernoulli equation for fluid flow:
where ρv 2/2 denotes kinetic energy, ρgh denotes gravitational potential energy and:
p = the fluid's static pressure ρ = the fluid's density v = the fluid's linear velocity g = the gravitational acceleration h = the height of a point on the centerline above any reference plane designated as having zero height.
For an incompressible fluid with a constant density and a venturi with a horizontal centerline, the equation simplifies to:[4]
or to:
Since the volumetric flow rate Q is the same at all points in the venturi by the continuity equation:[5]
then:
which can be re-arranged to:
The actual flow rate through a venturi tube is seldom equal to the theoretical flow rate of an ideal fluid and usually turns out to be less than the theoretical flow rate. In order to account for this difference, a discharge coefficient C is introduced to obtain the final volumetric flow rate equation for an incompressible fluid flowing through a venturi tube with a horizontal centerline:
where:
Q = the volumetric flow rate of the fluid C = the discharge coefficient = (actual flow rate) / (theoretical flow rate) A = the cross-sectional area of the venturi in the indicated section of the venturi p = the fluid's static pressure in the indicated section of the venturi ρ = the fluid's density
One method for determining the discharge coefficient is to calibrate the venturi tube on a test stand which is expensive and time consuming. A considerable number of test calibrations have been performed on various venturi tube geometries. As a result, the ASME Standard MFC-3M-1989[1] provides these discharge coefficients for their specified venturi tube geometry (per the diagram at the top of this article) and for three types of fabrication:[6][7]
- For venturi tubes with a welded convergent cone: C = 0.984 (valid for fluid flow Reynolds numbers between 2 × 105 and 6 × 106
- For venturi tubes with an as-cast convergent cone: C = 0.984 (valid for fluid flow Reynolds numbers between 2 × 105 and 6 × 106
- For venturi tubes with a machined convergent cone: C = 0.995 (valid for fluid flow Reynolds numbers between 2 × 105 and 2 × 106
[edit] Compressible fluid
For compressible fluids (i.e., a gases), the density is not constant. It will vary from the density ρ1 at the venturi inlet to the density ρ2 at the venturi throat. The equation for the mass flow rate of a compressible fluid through a venturi may be expressed as:[8][9]
The expansion factor Y allows for the change in gas density as the gas expands adiabatically from the venturi inlet pressure to the reduced pressure at the venturi throat. It may be calculated by using this equation:[8][9]
where:
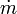
= mass flow rate Y = gas expansion factor C = the discharge coefficient A2 = cross-sectional area of the venturi's throat section ρ1 = the gas density in the venturi's inlet section p1 = the gas static pressure in the venturi's inlet section p2 = the gas static pressure in the venturi's throat section β = (A2/A1)1/2 for cylindrical tubes r = p2 / p1 k = the specific heat ratio of the gas
The above equation for calculating values of the expansion factor Y is valid for ρ2 / ρ1 > 0.75 and the uncertainity of a calculated value can be determined from:
As an example, for β = 0.65 and (P1 - P2) / P1 = 0.1, the uncertainty of Y is 0.72%.
[edit] Other uses for a venturi
Venturi tubes are used to create a low pressure or a partial vacuum in a great many applications (other than measuring flow rates) including the examples below as well as many others:
- Injectors or ejectors using steam, water, air or other motive fluid (liquid or gas) in a venturi to create a low pressure zone that draws in and entrains a suction fluid (liquid or gas).
- Water aspirators using water as a motive fluid to produce a partial vacuum.
- Atomizers using air as a motive fluid to spray paint, perfume or other liquids.
- Eductors using high-pressure water to create a partial vacuum to draw in and mix firefighting foam concentrate with the water.
- Carburetors using a gasoline combustion engine's intake air stream as the motive fluid to entrain and mix gasoline into intake air.
- Compressed air as the motive fluid to create the vacuum for industrial vacuum cleaners.
- Venturi scrubbers used in flue gas desulfurization systems.
- Sand blasters using compressed air to draw in fine sand in and mix it with air.
- A scuba diving regulator to assist the flow of breathing air once it starts flowing.
- In Venturi masks used in medical oxygen therapy.
- The De Laval nozzles used in rocket engines are essentially venturi tubes.
[edit] References
- ↑ 1.0 1.1 ASME Standard MFC-3M-1989, Measurement of Fluid Flow in Pipes Using Orifice, Nozzle, and Venturi', American Society of Mechanical Engineers (ASME), New York, 1989.
- ↑ Raymond A. Serway, Chris Vuille and Jerry S. Faughn (2008). College Physics, 8th Edition. Brooks Cole. ISBN 0-495-38693-6.
- ↑ Fluid Flow Parameters
- ↑ For points on the centerline of a horizontal venturi (constant h ), and since ρ is constant, ρgh is constant and equation 1 simplifies to equation 2. In fact, equation 1 simplifies to equation 2 for all points (on, above or below the horizontal centerline), because the potential energy terms ( ρgh ) vanish completely by designating a horizontal plane passing through the venturi's centerline as the level of zero potential energy. Volumes of mass above the centerline plane have positive potential energy equal to the negative potential energy of the volumes of mass below the plane and therefore the total potential energy is zero.
- ↑ A continuity equation in physics is an equation describing the transport of some kind of conserved quantity. Continuity equations are the (stronger) local form of the conservation laws. A conserved quantity cannot increase or decrease, it can only move from place to place.
- ↑ ORO-FLOW Users Guide
- ↑ Flowel 3.0 for Windows Flow Element Sizing and Documentation
- ↑ 8.0 8.1 Don W. Green and Robert H. Perry (19845-13). Perry's Chemical Engineers' Handbook, 6th Edition. McGraw-Hill. ISBN 0-07-049479-7. See equations 5-14 and 5-15 on pages 5-12 and 5-13.
- ↑ 9.0 9.1 E. John Finnemore and Joseph P. Franzini (2003). Fluid Mechanics with Engineering Applications, 10th Edition. McGraw-Hill. ISBN 7-302-06344-3. See pages 525-526
| |
Some content on this page may previously have appeared on Citizendium. |

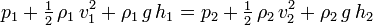
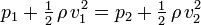
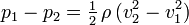
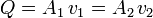
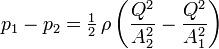
![Q = A_2 \sqrt {\frac {2\, (p_1 - p_2)}{\rho \left (1 - \left [\frac {A_2}{A_1} \right ]^2 \right)}}](../w/images/math/6/5/0/650871cee46a81439977e5c11107fca2.png)
![Q = C A_2 \sqrt {\frac {2\, (p_1 - p_2)}{\rho \left (1 - \left [\frac {A_2}{A_1} \right ]^2 \right)}}](../w/images/math/0/7/e/07e5bc92d1b610b9c9d489f05273f739.png)