Solid harmonics
In mathematics, solid harmonics are defined as solutions of the Laplace equation in spherical polar coordinates. There are two kinds of solid harmonic functions: the regular solid harmonics 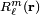 , which vanish at the origin, and the irregular solid harmonics
, which vanish at the origin, and the irregular solid harmonics 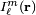 , which have an
, which have an 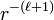 singularity at the origin. Both sets of functions play an important role in potential theory. Regular solid harmonics appear in chemistry in the form of s, p, d, etc. atomic orbitals and in physics as multipoles. Irregular harmonics appear in the expansion of scalar fields in terms of multipoles.
singularity at the origin. Both sets of functions play an important role in potential theory. Regular solid harmonics appear in chemistry in the form of s, p, d, etc. atomic orbitals and in physics as multipoles. Irregular harmonics appear in the expansion of scalar fields in terms of multipoles.
Both kinds of solid harmonics are simply related to spherical harmonics 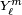 (normalized to unity),
(normalized to unity),
Contents |
[edit] Derivation, relation to spherical harmonics
The following vector operator plays a central role in this section
Parenthetically, we remark that in quantum mechanics 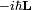 is the orbital angular momentum operator, where
is the orbital angular momentum operator, where  is Planck's constant divided by 2π. In quantum mechanics the momentum operator is proportional to the gradient,
is Planck's constant divided by 2π. In quantum mechanics the momentum operator is proportional to the gradient, 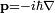 , so that L is proportional to r×p, the orbital angular momentum operator.
, so that L is proportional to r×p, the orbital angular momentum operator.
By using the relations
one can derive that
Expression in spherical polar coordinates gives:
and
It can be shown by expression of L in spherical polar coordinates that L² does not contain a derivative with respect to r. Hence upon division of L² by r² the position of 1/r² in the resulting expression is irrelevant. After these preliminaries we find that the Laplace equation ∇² Φ = 0 can be written as
It is known that spherical harmonics Yml are eigenfunctions of L²:
Substitution of Φ(r) = F(r) Yml into the Laplace equation gives, after dividing out the spherical harmonic function, the following radial equation and its general solution,
The particular solutions of the total Laplace equation are regular solid harmonics:
and irregular solid harmonics:
Racah's normalization (also known as Schmidt's semi-normalization) is applied to both functions
(and analogously for the irregular solid harmonic) instead of normalization to unity. This is convenient because in many applications the Racah normalization factor appears unchanged throughout the derivations.
[edit] Connection between regular and irregular solid harmonics
From the definitions follows immediately that
A more interesting relationship follows from the observation that the regular solid harmonics are homogeneous polynomials in the components x, y, and z of r. We can replace these components by the corresponding components of the gradient operator ∇. Thus, the left hand side in the following equation is well-defined:
For a proof see Biedenharn and Louck (1981), p. 312.
[edit] Addition theorems
The translation of the regular solid harmonic gives a finite expansion,
where the Clebsch-Gordan coefficient is given by
The similar expansion for irregular solid harmonics gives an infinite series,
with 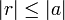 . The quantity between pointed brackets is again a Clebsch-Gordan coefficient,
. The quantity between pointed brackets is again a Clebsch-Gordan coefficient,
[edit] Real form
By a simple linear combination of solid harmonics of ±m these functions are transformed into real functions. The real regular solid harmonics, expressed in Cartesian coordinates, are homogeneous polynomials of order l in x, y, z. The explicit form of these polynomials is of some importance. They appear, for example, in the form of spherical atomic orbitals and real multipole moments. The explicit Cartesian expression of the real regular harmonics will now be derived.
[edit] Linear combination
We write in agreement with the earlier definition
with
where 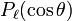 is a Legendre polynomial of order l.
The m dependent phase is known as the Condon-Shortley phase.
is a Legendre polynomial of order l.
The m dependent phase is known as the Condon-Shortley phase.
The following expression defines the real regular solid harmonics:
and for m = 0:
Since the transformation is by a unitary matrix the normalization of the real and the complex solid harmonics is the same.
[edit] z-dependent part
Upon writing u = cos θ the mth derivative of the Legendre polynomial can be written as the following expansion in u
with
Since z = r cosθ it follows that this derivative, times an appropriate power of r, is a simple polynomial in z,
[edit] (x,y)-dependent part
Consider next, recalling that x = r sinθcosφ and y = r sinθsinφ,
Likewise
Further
and
[edit] In total
[edit] List of lowest functions
We list explicitly the lowest functions up to and including l = 5 .
Here ![\bar{\Pi}^m_\ell(z) \equiv \left[\frac{(2-\delta_{m0}) (\ell-m)!}{(\ell+m)!}\right]^{1/2} \Pi^m_{\ell}(z) .](../w/images/math/4/b/d/4bd2d6d217543cf39461cc902a87a033.png)
The lowest functions 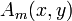 and
and 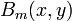 are:
are:
m Am Bm 0 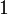
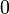
1 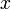
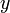
2 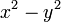
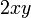
3 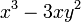
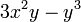
4 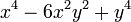
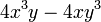
5 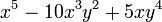
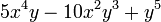
[edit] Examples
Thus, for example, the angular part of one of the nine normalized spherical g atomic orbitals is:
One of the 7 components of a real multipole of order 3 (octupole) of a system of N charges q i is
[edit] Spherical harmonics in Cartesian form
The following expresses normalized spherical harmonics in Cartesian coordinates (Condon-Shortley phase):
and for m = 0:
Here
and for m > 0:
For m = 0:
[edit] Examples
Using the expressions for 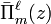 ,
, 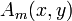 , and
, and 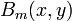 listed explicitly above we obtain:
listed explicitly above we obtain:
[edit] References
Most books on angular momenta discuss solid harmonics. See, for instance,
- D. M. Brink and G. R. Satchler, Angular Momentum, 3rd edition ,Clarendon, Oxford, (1993)
- L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, volume 8 of Encyclopedia of Mathematics, Addison-Wesley, Reading (1981)
The addition theorems for solid harmonics have been proved in different manners by many different workers. See for two different proofs for example:
- R. J. A. Tough and A. J. Stone, J. Phys. A: Math. Gen. Vol. 10, p. 1261 (1977)
- M. J. Caola, J. Phys. A: Math. Gen. Vol. 11, p. L23 (1978)


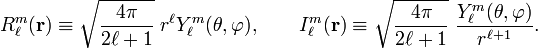
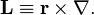
![L^2 \equiv \mathbf{L}\cdot\mathbf{L} = \sum_{i,j} [r_i\nabla_j r_i \nabla_j - r_i\nabla_j r_j \nabla_i]\quad \hbox{and}\quad \nabla_j r_i - r_i\nabla_j = \delta_{ji}](../w/images/math/1/a/3/1a3a6fcf64ed8f93ac41fbf313e1786a.png)
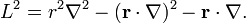
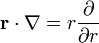
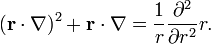
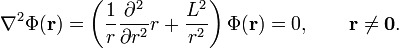
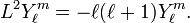
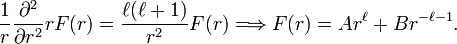
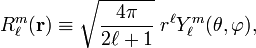
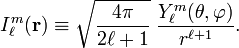
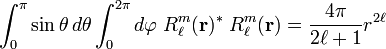
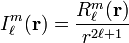
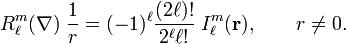
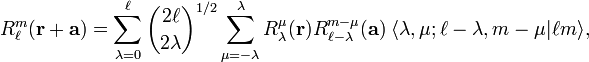
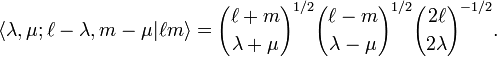
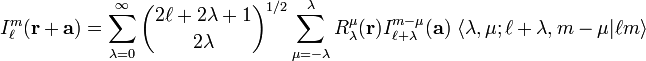
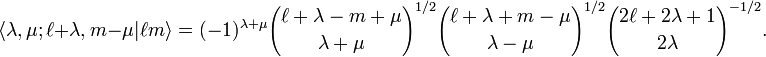
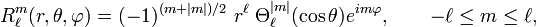
![\Theta_{\ell}^m (\cos\theta) \equiv \left[\frac{(\ell-m)!}{(\ell+m)!}\right]^{1/2} \,\sin^m\theta\, \frac{d^m P_\ell(\cos\theta)}{d\cos^m\theta}, \qquad m\ge 0,](../w/images/math/0/2/a/02a77c91241732ba10a075902a0aec1c.png)
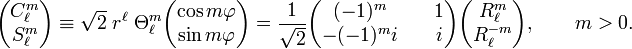
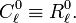
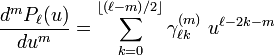
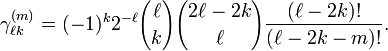
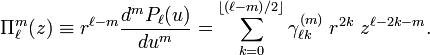
![r^m \sin^m\theta \cos m\varphi = \frac{1}{2} \left[ (r \sin\theta e^{i\varphi})^m
+ (r \sin\theta e^{-i\varphi})^m \right] =
\frac{1}{2} \left[ (x+iy)^m + (x-iy)^m \right]](../w/images/math/d/f/d/dfd1aea0e6f95b199e39761c6c8f0968.png)
![r^m \sin^m\theta \sin m\varphi = \frac{1}{2i} \left[ (r \sin\theta e^{i\varphi})^m
- (r \sin\theta e^{-i\varphi})^m \right] =
\frac{1}{2i} \left[ (x+iy)^m - (x-iy)^m \right].](../w/images/math/8/5/d/85d42914755b1347970e19483b6d5915.png)
![A_m(x,y) \equiv
\frac{1}{2} \left[ (x+iy)^m + (x-iy)^m \right]= \sum_{p=0}^m {m\choose p} x^p y^{m-p} \cos\left( (m-p) \frac{\pi}{2} \right)](../w/images/math/9/4/c/94c9cd653838af7f98215f108494fb0a.png)
![B_m(x,y) \equiv
\frac{1}{2i} \left[ (x+iy)^m - (x-iy)^m \right]= \sum_{p=0}^m {m\choose p} x^p y^{m-p} \sin\left( (m-p) \frac{\pi}{2}\right).](../w/images/math/f/d/1/fd1e5af517ff764172e81feafebef029.png)
![C^m_\ell(x,y,z) = \left[\frac{(2-\delta_{m0}) (\ell-m)!}{(\ell+m)!}\right]^{1/2} \Pi^m_{\ell}(z)\;A_m(x,y),\qquad m=0,1, \ldots,\ell](../w/images/math/4/2/8/428a7f7aff8aec77ae8b00ff442526fc.png)
![S^m_\ell(x,y,z) = \left[\frac{2 (\ell-m)!}{(\ell+m)!}\right]^{1/2} \Pi^m_{\ell}(z)\;B_m(x,y)
,\qquad m=1,2,\ldots,\ell.](../w/images/math/d/b/6/db64065a519539ef5a9a3a26d49d0d0e.png)
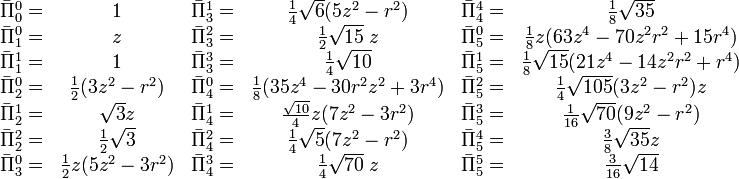
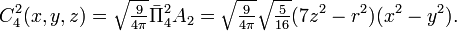
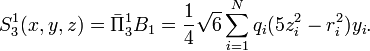
![r^\ell\,
\begin{pmatrix}
Y_\ell^{m} \\
Y_\ell^{-m}
\end{pmatrix}
=
\left[\frac{2\ell+1}{4\pi}\right]^{1/2} \bar{\Pi}^m_\ell(z)
\begin{pmatrix}
(-1)^m (A_m + i B_m)/\sqrt{2} \\
\qquad (A_m - i B_m)/\sqrt{2} \\
\end{pmatrix} ,
\qquad m > 0.](../w/images/math/7/a/9/7a93ad400213dce27d80945e4107996a.png)
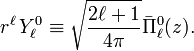
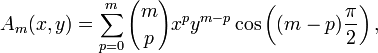
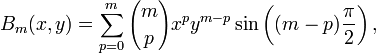
![\bar{\Pi}^m_\ell(z)
= \left[\frac{(\ell-m)!}{(\ell+m)!}\right]^{1/2}
\sum_{k=0}^{\left \lfloor (\ell-m)/2\right \rfloor}
(-1)^k 2^{-\ell} {\ell\choose k}{2\ell-2k \choose \ell} \frac{(\ell-2k)!}{(\ell-2k-m)!}
\; r^{2k}\; z^{\ell-2k-m}.](../w/images/math/5/3/8/538c86df07273c67c93527733924022a.png)
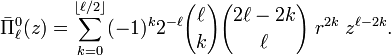
![Y^1_3 = - \frac{1}{r^3} \left[{\textstyle \frac{7}{4\pi}\cdot \frac{3}{16} }\right]^{1/2} (5z^2-r^2)(x+iy) =
- \left[{\textstyle \frac{7}{4\pi}\cdot \frac{3}{16}}\right]^{1/2} (5\cos^2\theta-1) (\sin\theta e^{i\varphi})](../w/images/math/0/c/f/0cfcaba8e10d545aca1c19dd13535ca6.png)
![Y^{-2}_4 = \frac{1}{r^4} \left[{\textstyle \frac{9}{4\pi}\cdot\frac{5}{32}}\right]^{1/2}(7z^2-r^2) (x-iy)^2
= \left[{\textstyle \frac{9}{4\pi}\cdot\frac{5}{32}}\right]^{1/2}(7 \cos^2\theta -1) (\sin^2\theta e^{-2 i \varphi})](../w/images/math/3/3/5/3354182ef30cc56d09101c49537dd663.png)