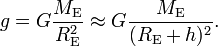Weight
Weight is a property of objects in a gravitational field. The weight of an object of non-zero mass is the force exerted on it by a gravitational field, usually a field caused by a single very large (planet-sized) object. The gravitational force (weight) acting on an object is directly proportional to the mass of the object.
On earth, the weight of an object of mass m (expressed in kilogram) is to a good approximation equal to the force 10×m N (newton).[1]
[edit] Details
Newton's law of gravitation gives the force f exerted by two objects on each other. When the objects are of mass M1 and M2, respectively, and the distance between the centers of mass of the objects is R, then:
where the force f is a vector along the line that connects the centers of mass of the two objects. The direction of f is such that the objects always attract each other. The factor G is a natural constant, for obvious reasons called the gravitational constant.
By application of Newtons' law one finds that at a height h above the surface of the earth, the weight of an object is equal to its mass multiplied by a product of G, the mass ME of the earth, and the inverse squared distance of the object to the center of mass of the earth. This product is usually indicated by the symbol g, the gravitational acceleration on the surface of the earth,
It is assumed that h << RE (height h of object above the surface of the earth is much less than the radius of the earth, RE ≈ 6400 km), so that g and the weight mg of an object of mass m are independent of height. There are minor local variations in g ≈ 9.8 m/s² due to the irregularity of the earth's surface and density.
On other planets, with different total mass and radius (but same G), the weight of an object of a given mass will be different from its weight on earth, and thus accelerating the object will require different amounts of force. Most sources of force are not dependent on their weight, and so most actions will have different results in different gravitational fields. The classic example of this is a person jumping on different planets. Due to the different gravitational fields of the different planets, the person's weight will be different, but the force produced by his muscles will be essentially the same, as the force is produced by a chemical reaction. Therefore, a person can jump significantly higher in a weaker gravitational field, such as occurs on earth's moon, but will be unable to jump as high in a stronger gravitational field, such as occurs on Jupiter.
[edit] Units
In SI units, weight is measured in units of force, the newton and its derivatives. In U.S. customary units, weight is measured in pounds and other units which are fractions or multiples of the pound. The pound is the force of 0.453 592 37 kg subject to a standard gravity of 9.80665 m s−2, or approximately 4.448 N.
[edit] Note
- ↑ Although the third Conférence Générale des Poids et Mesures declared as early as 1901 that the statement "I weigh 70 kg" is better replaced by "my mass is 70 kg", or "I weigh 700 N", nobody says this outside a physics class room.
| |
Some content on this page may previously have appeared on Citizendium. |