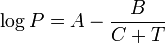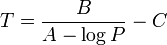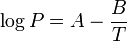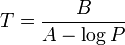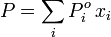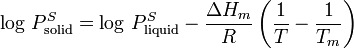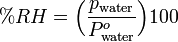Vapor pressure
Vapor pressure (also known as equilibrium vapor pressure), is the pressure of a vapor in equilibrium with its liquid or solid phase.[1][2] At any given temperature, for a specific substance, there is a pressure at which the gas of that specific substance is in dynamic equilibrium with its liquid or solid forms. This is the vapor pressure of the specific substance at that temperature.
The vapor pressure of a substance increases with increasing temperature.
Contents |
[edit] Volatility of liquids
The vapor pressure is an indication of a liquid's evaporation rate. It relates to the tendency of molecules and atoms to escape from a liquid or a solid. A substance with a high vapor pressure at normal temperatures is often referred to as volatile.
Relative volatility is a measure that compares the vapor pressures of the components in a liquid mixture of chemicals. This measure is widely used in designing large industrial distillation, absorption and other separation processes that involve the contacting of vapor and liquid phases in a series of equilibrium stages.[3][4][5] In effect, it indicates the ease or difficulty of separating the more volatile components from the less volatile components in a liquid mixture.
[edit] Calculating vapor pressures with Antoine equation
The Antoine equation [6][7] is a mathematical expression of the relation between the vapor pressure and the temperature of pure substances. The basic form of the equation is:
and it can be transformed into this temperature-explicit form:
where: P is the absolute vapor pressure of a substance
- T is the temperature of the substance
- A, B and C are substance-specific coefficients (i.e., constants or parameters)
- log is typically either log10 or loge
A simpler form of the equation with only two coefficients is sometimes used:
which can be transformed to:
[edit] Vapor pressures and normal boiling points of liquids
The atmospheric pressure boiling point of a liquid (also known as the normal boiling point) is the temperature where the vapor pressure equals the ambient atmospheric pressure. With any incremental increase in that temperature, the vapor pressure becomes sufficient to overcome atmospheric pressure and lift the liquid to form bubbles inside the bulk of the substance. Bubble formation deeper in the liquid requires a higher pressure, and therefore higher temperature, because the fluid pressure becomes higher than atmospheric pressure as the depth increases.
The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point (i.e., the boiling point at atmospheric pressure) of the liquid.
The vapor pressure chart to the right has graphs of the vapor pressures versus temperatures for a variety of liquids.[4] As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points.
For example, at any given temperature, methyl chloride has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point (– 26 °C), which is where the vapor pressure curve of methyl chloride (the blue line) intersects the horizontal pressure line of one atmosphere (atm) of absolute vapor pressure.
Although the relation between vapor pressure and temperature is non-linear, the chart uses a logarithmic vertical axis in order to obtain slightly curved lines so that one chart can graph many liquids.
[edit] Units of vapor pressure
The international SI unit for pressure is the pascal (Pa), equal to one newton per square meter (N·m-2 or kg·m-1·s-2). The conversions to other pressure units are: Template:Pressure
[edit] Vapor pressure of liquid mixtures
Raoult's law gives an approximation to the vapor pressure of mixtures of liquids.[1][2] It states that the vapor pressure of a liquid mixture is equal to the mole-fraction-weighted sum of the vapor pressures of the mixture's pure components:
| where: | |
| P | = vapor pressure of a liquid mixture |
|---|---|
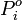
|
= vapor pressure of pure component i in the liquid mixture |
| xi | = mole fraction of component i in the liquid mixture |
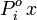
|
= pi = the partial pressure of component i in the liquid mixture |
Raoult's law is applicable only to ideal liquids and to components that are fairly similar such as benzene and toluene, hexane and heptane or o-xylene and p-xylene.
Systems that have vapor pressures higher than indicated by the above equation are said to have positive deviations. Such a deviation suggests weaker intermolecular attraction than in the pure components, so that the molecules can be thought of as being "held in" the liquid phase less strongly than in the pure liquid. An example is the azeotrope of approximately 95% ethanol and water. Because the azeotrope's vapor pressure is higher than predicted by Raoult's law, it boils at a temperature below that of either pure component.
There are also systems with negative deviations that have vapor pressures that are lower than expected. Such a deviation is evidence for stronger intermolecular attraction between the constituents of the mixture than exists in the pure components. Thus, the molecules are "held in" the liquid more strongly when a second molecule is present. An example is a mixture of trichloromethane (chloroform) and 2-propanone (acetone), which boils above the boiling point of either pure component.
[edit] Vapor pressure of solids

All solid materials have a vapor pressure which, for most solids, is very low. Some notable exceptions are naphthalene, ice and dry ice (carbon dioxide). The vapor pressure of dry ice is 5.73 MPa (56.5 atm) at 20 °C which would cause most sealed containers to rupture.
Due to their often extremely low values, measurement of the vapor pressure of solids can be rather difficult. Typical techniques for such measurements include the use of thermogravimetry and gas transpiration.
The vapor pressure of a solid can be defined as the pressure at which the rate of sublimation of a solid matches the rate of deposition of its vapor phase.
There are a number of methods for calculating the sublimation pressure (i.e., the vapor pressure) of a solid. One method is to calculate sublimation pressures [8] from extrapolated liquid vapor pressures if the heat of fusion is known. The heat of fusion has to be added in addition to the heat of vaporization to vaporize a solid. Assuming that the heat of fusion is temperature-independent and ignoring additional transition temperatures between different solid phases, the sublimation pressure can be calculated using this version of the Clausius-Clapeyron equation:
where: 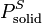
= Sublimation pressure of the solid component at the temperature 
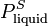
= Extrapolated vapor pressure of the liquid component at the temperature 
ΔHm = Heat of fusion R = Universal gas constant T = Sublimation temperature Tm = Melting point temperature
gives a fair estimation for temperatures not too far from the melting point. This equation also shows that the sublimation pressure is lower than the extrapolated liquid vapor pressure (ΔHm is positive) and the difference increases with increased distance from the melting point.
[edit] Relative humidity
The ratio, often expressed as a percentage, of the partial pressure of water in the atmosphere at some observed temperature, to the vapor pressure of pure water at this temperature.[9] It may be expressed as:
| where: | |
| %RH | = percent relative humidity of the atmospheric air-water mixture |
| pwater | = partial pressure of water in the atmospheric air-water mixture |

|
= vapor pressure of pure water at the temperature of the atmospheric air-water mixture |
At 100 percent relative humidity, the atmospheric air is said to be saturated with water. That occurs when the partial pressure of the water in the air, pwater, is equal to the vapor pressure of pure water at the air temperature,  .
.
Given the wet-bulb temperature and the dry-bulb temperature of the atmosphere, which are readily measured by using a sling psychrometer, the relative humidity can be obtained from a psychrometric chart.[4]
[edit] Vapor pressure terminology in meteorology
The terminology defined and discussed in this article is the terminology used extensively by chemists, chemical engineers and others.
The terminology used by workers in the field of meteorology is unique to that field of science and it defines vapor pressure and similar terms quite a bit differently than is done in this article. For example, the American Meteorological Society (AMS) uses the following definitions:[10]
- Vapor pressure: The portion of the total air pressure exerted by the water vapor component of air. (That would be the partial pressure of the water vapor in the air using the terminology defined in this article.)
- Saturation vapor pressure: The maximum vapor pressure in a sample of air at a specific temperature. (That is not the meaning of "saturation vapor pressure" as defined in this article. In the terminology defined in this article, it can be said that air at a specific temperature is saturated when the partial pressure of the water in the air is equal to the vapor pressure of pure water at that specific temperature. In other words, when relative humidity is 100%.)
To avoid any confusion, this article makes no attempt to go into any further detail concerning the terminology used in meteorology.
[edit] References
- ↑ 1.0 1.1 Neil D. Jesperson (1997). Chemistry. Barron's Educational Series. ISBN 0-8120-9503-0.
- ↑ 2.0 2.1 Robert G. Mortimer (2008). Physical Chemistry, 3rd Edition. Academic Press. ISBN 0-12-370617-3.
- ↑ Kister, Henry Z. (1992). Distillation Design, 1st Edition. McGraw-hill. ISBN 0-07-034909-6.
- ↑ 4.0 4.1 4.2 Perry, R.H. and Green, D.W. (Editors) (1984). Perry's Chemical Engineers' Handbook, 6th Edition. McGraw-hill. ISBN 0-07-049479-7.
- ↑ Seader, J. D., and Henley, Ernest J. (1998). Separation Process Principles. New York: Wiley. ISBN 0-471-58626-9.
- ↑ What is the Antoine Equation? (Chemistry Department, Frostburg State University, Maryland)
- ↑ R.K.Sinnot (2005). Chemical Engineering Design, 4th Edition. Butterworth-Heinemann. ISBN 0-7506-6538-6.
- ↑ Bruce Moller, Jürgen Rarey and Deresh Ramjugernath (2008). "Estimation of the vapour pressure of non-electrolyte organic compounds via group contributions and group interactions". J.Molecular Liquids 143 (1): 52-63.
- ↑ Relative Humidity IUPAC Compendium of Chemical Terminology (Electronic version)
- ↑ AMS Glossary of Atmospheric Terms
| |
Some content on this page may previously have appeared on Citizendium. |