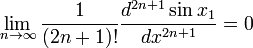Sine
In trigonometry, the function sine and its complementary function cosine, abbreviated sin and cos, are central. They are used to express relations between angles and sides of triangles. The functions are very common and important in all branches of science and technology. It is possible to define sine and cosine in different ways. Two ways, one based on plane geometry and one based on differential equations, will be discussed below.
Contents |
[edit] Geometric approach
In most countries, schoolchildren begin to study mathematics with arithmetics, elementary algebra and 2-dimensional Euclidean geometry (plane geometry). [1] When they learn about sin and cos, the students already have some idea about addition and measurement of angles, segments and areas; they already have accepted the axioms of Euclid and they know the Pythagorean theorem. Therefore, the trigonometric functions are defined as ratios of the lengths of sides of right-angled triangles. We will outline this approach, but point out that an alternative approach is possible which does not rely on Euclid's axioms. This approach, which is more advanced in that it needs some knowledge of differential calculus, will be given in a later section.
[edit] Definition of sine and cosine in plane geometry
The most elementary definition of the functions sine and cosine follows from Fig. 1. We see a right-angled triangle ABC (black) with an acute angle α. By definition sinα is equal to the the length a of the side opposite angle α divided by the hypotenuse, which has length b. The cosine of α is the length c of the side adjacent to α divided by the length of the hypotenuse b:
Applying the same definitions to the complementary angle ∠DAC (= 90°−α) we find from the dashed blue triangle in Fig. 1,
We see that for complementary angles the functions sine and cosine are interchanged, hence the name "cosine" (short for "complementary sine").
The Pythagorean theorem states that b2 = a2+c2, so that we get the following important relation between the sine and the cosine functions
Since this elementary definition of sine and cosine is in terms of ratios of lengths, which are positive, the definition needs to be generalized in order to account for negative function values.
[edit] Cartesian definition
We recall that a vector r in a 2-dimensional plane can be represented by two Cartesian coordinates, which are real numbers: r = (x, y). These numbers are the projections of r on the x- and the y-axis, respectively. The length of r is denoted by |r| and is defined by
Assuming that the length of r is non-zero we can divide the components of the vector by it and obtain a unit vector er, which by definition has length unity. Unit vectors in the plane have their endpoints on a unit circle (circle with unit radius).
Consider Fig. 1 again. Assume now that the length b equals 1, then the vector eAC pointing from point A to point C is a unit vector. Assume a Cartesian system of axes with the origin in A and let the x-axis be along A–B and the y-axis be along A–D. Clearly cosα = c is the projection of eAC on the x-axis, i.e., cosα = c is the x-coordinate of this unit vector. Similarly sinα = a is the y coordinate of the unit vector. This observation leads to the following definition, which is a generalization of the earlier one.
Write ex for a unit vector on the x-axis and ey for a unit vector on the y-axis.
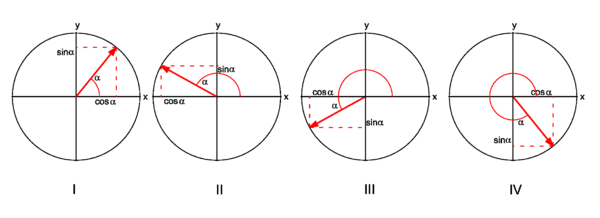
Definition: If e is a unit vector obtained from ex by a positive (counter-clockwise) rotation over the angle α, then cosα is the x coordinate of e and sinα is the y coordinate of e:
The unit vector e is depicted (as a red vector with endpoint on the unit circle) in the four different quadrants in Fig. 2.
| | |||
|
Signs of sine and cosine | |||
| Quadrant | Range α | cos | sin |
| | |||
| I | 00< α < 900 | + | + |
| II | 900< α < 1800 | − | + |
| III | 1800< α < 2700 | − | − |
| IV | 2700< α < 3600 | + | − |
Clearly, if α=0° then e = ex. If α=90° then e = ey. If α=180° then e = −ex. Thus,
It is also clear from the definition that, when α is rotated over more than 360°, the unit vector is back at an angle between 0° and 360°. Therefore, for positive integer k,
Negative angles are defined by rotating the unit vector clockwise. By definition reflection in the x-axis changes the components of the unit vector thus,
Further one sees easily that α is mapped to −α under this reflection. That is, upon reflection α and the y-coordinate change sign and the x-coordinate is invariant (stays the same), hence
When one rotates the unit vector clockwise over more than 360° one arrives again at a position between 0° and 360°, so that for positive integer k,
By standard arguments of plane Euclidean geometry one can compute the numerical values of sine and cosine for a few specific angles. The application of differential calculus (see later in this article) allows the computation of the function values for all angles. Thus, one obtains the graphs shown in Fig. 3.
[edit] Sum formulas
The following equations hold:
Proof
The proof is easiest in matrix notation. Because we do not expect readers to know this notation we give the proof in long-hand notation and only indicate briefly the equivalent matrix form. The unit vectors and angles that play a role in the proof are depicted in Fig. 4.
As shown in Fig. 4A, the singly primed (green) unit vectors are given in terms of the unprimed (black) unit vectors by
In Fig. 4B the doubly primed (red) unit vector ex " is given in terms of the singly primed (green) unit vectors by
In Fig. 4C the doubly primed (red) vector ex " is given in terms of the unprimed (black) vectors:
Substitution of the expression for the singly primed unit vectors (green) in terms of the unprimed vectors (black) into the expression for ex " gives :
Upon rearranging,
(In matrix notation the last two expression are equivalent to the multiplication of a row vector with a square matrix). Putting Eqs. (1) and (2) for ex " in terms of the unprimed unit vectors side by side, we find the equations to be proved. This conclusion is allowed because ex and ey are linearly independent.
[edit] Sine rule
- See law of sines.
If α, β, and γ are the angles of a triangle and a, b, and c the lengths of the respective opposite sides, then the law of sines (sine rule) states
where d is the diameter of the circumscribed circle of the triangle.
[edit] Series expansion
The Taylor expansion of sin x around the point x = 0 will be given.
The first derivative of the sine function is the cosine, and the first derivative of the cosine is minus the sine,
From this,
From sin(0) = 0, cos(0) = 1 it follows that the (4n + k)-th derivatives of the sine at the point 0 (n a natural number and k = 0, 1, 2, 3) are given by:
Knowing this, one may write the Taylor series as follows,
This is the Taylor series expansion at x = 0. Taylor's theorem states that a necessary and sufficient condition for the Taylor expansion of sin to converge to sin x for all x ∈ ℝ is that
for some point x1. Thus, the convergence of the Taylor series is due to the fact that the derivatives of sin x are bounded for any x (sin x1 is between −1 and 1 for any x1), while the factor 1/(2n+1)! goes to zero. The Taylor expansion of sin x is valid on the whole real line.
[edit] Notes
- ↑ A. P. Kiselev (1892 (first edition in Russian)). Elementary Geometry for Secondary Educational Institutions. ISBN 0-9779852-0-2.
| |
Some content on this page may previously have appeared on Citizendium. |





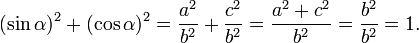
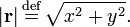
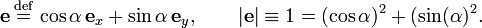
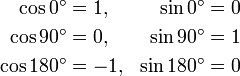





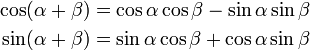

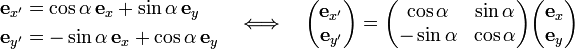


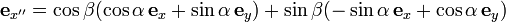
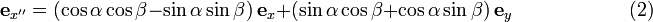
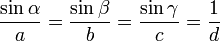
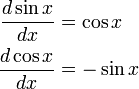
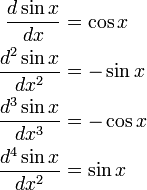
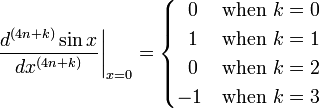
![\begin{align}
\sin x & = \sum_{n=0}^\infty \sum_{k=0}^3
\frac{1}{(4n+k)!} \left. \frac{d^{4n+k} \sin x}{dx^{4n+k}} \right|_{x=0} x^{4n+k} \\
& = \sum_{n=0}^\infty\left[
\frac{1}{(4n+1)!} x^{4n+1} - \frac{1}{(4n+3)!} x^{4n+3} \right]
\\
& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1}, \\
& = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} \cdots \\
\end{align}](../w/images/math/9/b/b/9bb5615a98a64be890e889ff35dceedb.png)