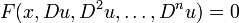Partial differential equation

From Knowino
Jump to: navigation, search

A partial differential equation, or a PDE, is an equation giving a relationship between a function of multiple variables and its derivatives. Any function satisfying this equation is known as a solution of the PDE.

The theoretical study of PDEs focuses on the notion of "well posedness," while the actual calculation of solutions is a staple of numerical analysis. There is no general theory concerning the solutions of PDEs, as there are for ordinary differential equations (ODEs). Rather, PDEs are classified by particular properties of each equation, among which are order, linearity, and other more specific criteria.

PDEs have vast application throughout the sciences and related disciplines. They are used to formulate the laws of nature and to model numerous kinds of probabilistic, dynamic, and static phenomena. Although the actual processes being studied can be quite different, there are often startling similarities and even congruences in their mathematical description, allowing techniques originally inspired by the study of one phenomenon to rapidly yield insights on another.

[edit] Formal statement

Formally, on an open set 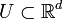U \subset \mathbb{R}^d, a PDE is most generally written as

F(x,Du,D^2 u, \ldots, D^n u) = 0

where u is the desired solution to the equation, the order n of the equation is the order of the highest derivative of u to appear, and F is a given function:

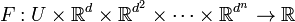F: U \times \mathbb{R}^d \times \mathbb{R}^{d^2} \times \cdots \times \mathbb{R}^{d^n} \rightarrow \mathbb{R}.

By convention, u takes on values in the real numbers. If u is vector-valued, the problem is reducible to a collection of separate conditions on each individual component of u, and the problem is referred to as a system of partial differential equations.

[edit] Well posedness

The theory of PDEs centers around showing that particular problems are "well posed." A problem consists of the PDE and accompanying data, which are usually inputs such as initial conditions, boundary conditions, or other information needed to precisely specify the process being modeled. The type of data required depends on the equation.

The notion of "well posedness" is a heuristic one. Broadly speaking it consists of showing that solutions to a particular problem possess the properties of

  1. Existence
  2. Uniqueness
  3. Continuous response to continuous perturbations in data.

[edit] Notes

Information.svg Some content on this page may previously have appeared on Citizendium.
Retrieved from "http://knowino.org/wiki/Partial_differential_equation"
Personal tools
Variants
Actions
Navigation
Community
Toolbox