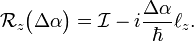Orbital-angular momentum
In quantum mechanics, orbital angular momentum is a conserved property of a system of one or more particles that move in a centrally symmetric potential. An example is given by an atom: an atom consists of a number of electrons moving in the central field of a single nucleus. If the position of particle k with respect to the center of symmetry is rk = (xk, yk, zk) and if the momentum of the same particle is pk, then the orbital angular momentum of particle k is defined by
where the symbol × indicates the cross product of two vectors. The total angular momentum of a system of N particles is
In the x-representation of quantum mechanics,[1] the components of the vector rk are seen as multiplicative operators and the momentum of particle k is replaced by a differential vector operator,
Note that the following relation, valid for the cross product of classical vectors, also holds for the corresponding quantum mechanical quantities,
In the p-representation of quantum mechanics r is replaced by a differentiation with respect to p (note the sign),
and the components of p are handled as multiplicative operators. It is uncommon to study angular momenta in the p-representation, and this approach will not be pursued further in this article.
Given two linear operators, A and B, mapping the same linear space into itself, a multiplication AB between the two is defined by applying first B and then A to an element of the space. This ordinary operator multiplication gives rise to a new product, called the Lie, or commutator, product, notated by square brackets:
Since A and B are linear AB and BA are linear, too, and their difference is well-defined. If [A,B] = 0, the operators A and B are said to commute. Clearly, the Lie product is antisymmetric, that is, [A, B] = −[B, A]. The commutator product of linear operators plays an important role in quantum mechanics and in Lie theory, a branch of mathematics that is called after the Norwegian mathematician Sophus Lie (1842 – 1899).
The components of the orbital angular momentum (from here on in the x-representation) satisfy the following commutator (Lie) products,
The fact that L is a conserved quantity is expressed by the commutation with the Hamiltonian (energy operator)
It can be shown that this condition is necessary and sufficient that the potential energy part of H be centrally symmetric.
Contents |
[edit] Lie algebra
The three components 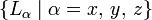 of the quantum mechanical orbital-angular momentum span a Lie algebra. This statement will be explained in this section.
of the quantum mechanical orbital-angular momentum span a Lie algebra. This statement will be explained in this section.
[edit] Definition of Lie algebra
The commutator (Lie) product mentioned above—more in particular the fact that the three orbital-angular momentum operators are closed under this product—together with the fact that a linear combination 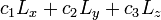 (with
(with 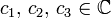 ) is a well-defined linear operator, shows that the three operators span a three-dimensional linear space that is closed under the Lie product. Such a set is an algebra.
) is a well-defined linear operator, shows that the three operators span a three-dimensional linear space that is closed under the Lie product. Such a set is an algebra.
The algebra spanned by 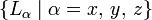 satisfies the Jacobi identity. This holds for any algebra consisting of linear operators.
To show this, consider three arbitrary linear operators, A, B, and C, acting on the same space so that the ordinary operator multiplication giving AB, BC, etc., between them is defined. The following cyclic relation (the Jacobi relation) holds,
satisfies the Jacobi identity. This holds for any algebra consisting of linear operators.
To show this, consider three arbitrary linear operators, A, B, and C, acting on the same space so that the ordinary operator multiplication giving AB, BC, etc., between them is defined. The following cyclic relation (the Jacobi relation) holds,
where the square brackets again indicate commutator products. The proof of the Jacobi identity follows directly from the following properties,
Using in both terms of the right-hand side the antisymmetry of the Lie product, the Jacobi identity identity follows. Note, parenthetically, that the Lie product is not associative,
An algebra satisfying the Jacobi identity and the properties that are obviously satisfied by the commutator product:
is a Lie algebra. It follows that the linear span of the orbital-angular momentum operators 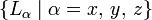 is a Lie algebra.
is a Lie algebra.
[edit] Lie algebra of full rotation matrix group
Usually Lie algebras are associated with Lie groups. The Lie algebra spanned by the components of the orbital-angular momentum, is associated with the full rotation group in three dimensions, often indicated by SO(3) (a Lie group). A common definition of SO(3) is as matrix group. It is the Special group consisting of real 3×3 Orthogonal matrices. The adjective "special" refers in this context to the matrices in SO(3) having unit determinant.
The Lie algebra of SO(3) consists of all possible real 3×3 antisymmetric matrices.[2] The space of such matrices forms a Lie algebra spanned by the derivatives (at angle zero) of the following three elements of SO(3), representing rotations around the x, y, and z-axis, respectively,
Since antisymmetric matrices have zero diagonal and only the elements below the diagonal are free to choose (the elements above the diagonal follow by transposition), the three matrices Kx, Ky, and Kz form a basis for the 3-dimensional linear space of antisymmetric matrices. By ordinary matrix multiplication one verifies that [Kx, Ky] = KxKy - KyKx = Kz, etc., so that the set of antisymmetric matrices form a Lie algebra, the Lie algebra of the matrix group SO(3).
The Lie algebra of SO(3) is almost isomorphic with the Lie algebra spanned by orbital-angular momentum operators. The algebras become isomorphic when we define
and consider the Lie algebra spanned by the matrices Mα.
While the matrices K are antisymmetric, the matrices M are Hermitian, that is Mi,j = Mj,i∗, where ∗ stands for complex conjugation of a complex number.
So, there is an algebra isomorphism (one-to-one, multiplication preserving) between the Lie algebras spanned by the operators 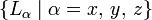 and by the matrices
and by the matrices 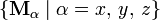 . However, the algebras consist of completely different objects. The former are linear operators on a space of functions (an infinite dimensional Hilbert space) and the latter are 3×3 matrices, that are—if you wish—linear operators on a three dimensional vector space.
. However, the algebras consist of completely different objects. The former are linear operators on a space of functions (an infinite dimensional Hilbert space) and the latter are 3×3 matrices, that are—if you wish—linear operators on a three dimensional vector space.
[edit] Lie derivatives
In this section it will be shown that the three components of the one-particle orbital-angular momentum operator are (up to the factor 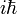 ) equal to so-called Lie derivatives. The Lie derivatives form a Lie algebra that (apart from the factor) is isomorphic to the Lie algebra spanned by the
) equal to so-called Lie derivatives. The Lie derivatives form a Lie algebra that (apart from the factor) is isomorphic to the Lie algebra spanned by the 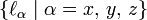
[edit] Definition of full rotation group in terms of Hilbert space operators
In order to relate the orbital-angular momentum operators (that act on a Hilbert space of functions) to the full rotation group SO(3), other than by the observation that the linear operators 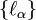 and
and 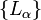 are in 1-1 correspondence with the 3×3 matrices Mα, it is necessary to redefine SO(3) from a group of matrices to a group of operators acting on the same Hilbert space as the orbital-angular momenta
are in 1-1 correspondence with the 3×3 matrices Mα, it is necessary to redefine SO(3) from a group of matrices to a group of operators acting on the same Hilbert space as the orbital-angular momenta 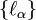 .
.
This needs the following definitions. First let r = (r1, r2, r3)T be a real column vector and let R be a real 3×3 orthogonal matrix with unit determinant, a proper rotation matrix. The inverse of R is well-defined. Let ψ(r) be a real- or complex-valued function defined on all of 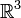 . A rotation operator
. A rotation operator 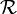 acting on ψ is defined by
acting on ψ is defined by
The inverse rotation matrix appears here to preserve multiplication order in the map from matrix to operator:
The set 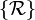 forms a group that is a homomorphic image of the matrix group SO(3). If, for instance, a function space is considered consisting of one spherically symmetric function ψ the group
forms a group that is a homomorphic image of the matrix group SO(3). If, for instance, a function space is considered consisting of one spherically symmetric function ψ the group 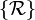 consists of one element only: the identity. However, usually the function spaces considered are so large that there is an isomorphism, and it is common to assume this, and to denote the set of rotation operators also by SO(3).
consists of one element only: the identity. However, usually the function spaces considered are so large that there is an isomorphism, and it is common to assume this, and to denote the set of rotation operators also by SO(3).
[edit] Redefinition of Lie algebra of SO(3) in terms of Lie derivatives
As above, one passes from a Lie group to its Lie algebra by differentiating at zero angle, but this time a rotated function is differentiated. In this differentiation one needs to assume that the rotated function is differentiable for any rotation. Because a rotation is characterized by three angles α, β, γ, partial derivatives will appear. In handling partial derivatives it is convenient to avoid differentials by introducing the "time" t, and to assume that the rotation angles are functions of t: α(t), β(t), and γ(t), such that α(0) = β(0) = γ(0) = 0. The zero rotation angles parametrize the identity rotation 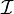 in SO(3).
in SO(3).
Any rotation operator acting on functions ψ(r) can be written as a function of three angles,
The set
is a curve in the operator group SO(3). Differentiation at t = 0 gives the tangent of the curve at the identity. It will be shown that the tangent of any curve can be expressed linearly in terms of the three orbital-angular momentum operators, or in other words, the tangent space at the identity of the operator group SO(3) has as basis 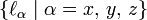 .
.
To prove this, it is noted that an arbitrary rotation can be factored in rotations around x, y, and z, successively (see this article for a proof). The order of factors is not unique (but different order gives different angles) and the factors do not commute because the rotations are around different axes. However, after differentiation one obtains a tangent vector of the curve that does not depend on the order, and hence we may write without loss of generality,
Consider
By the chain rule, using the short-hand notation s(t) = R(t)−1 r and noting that for t = 0, s(0) = r, one gets
where ∇ is the nabla operator introduced above, and a dot above a symbol stands for a time derivative of the symbol.
The differentiation of s(t) = R(t)−1r at t = 0 is simple. Indeed, on the one hand,
On the other hand by the product rule of differentiation (that holds for matrix products) and using that R(0) = R(0)−1= I, one finds
so that
Then,
because, again, the matrices Rz(α(t))=Rz(t), etc. are identity matrices for t = 0.
By the chain rule
where the matrix Kz was introduced in the previous section. Analogous expressions hold for the differentiation of the other two matrices and one obtains
where the tangent vector in the linear space spanned by Kx, Ky, Kz is given by the component vector ω,
Note that matrix multiplication in the group is associated with matrix addition in the Lie algebra spanned by the matrices Kx, Ky, and Kz. This association is analogous to the multiplication of ordinary exponential functions
The analogy is no coincidence, below it will be shown that the elements of the rotation group can be written as (products of) exponential functions.
By the use of the explicit forms of the antisymmetric matrices Kα given in the previous section and by inspection:
where × stands for a vector product, which is antisymmetric in its factors. Using Eq. (1) one obtains
where in the last equality a well-known property of the vector triple product is applied.
In group theory the operator ω⋅(r×∇) (acting on ψ) is known as the Lie derivative of ψ along the tangent ω at the identity. The Lie derivative is sometimes written as 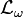 .[3] The general definition of the Lie derivative of the Lie group SO(3) is:
.[3] The general definition of the Lie derivative of the Lie group SO(3) is:
where the curve R(t) passes through the identity matrix R(0) = I with tangent ω.
Remember that
forms a Lie algebra, and the final equation
gives the relation between the Lie algebra spanned by the orbital-angular momentum operators 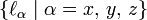 and the rotation group SO(3) consisting of operators
and the rotation group SO(3) consisting of operators 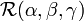 . The function ψ does not play any role and is dropped from the equation. The rotation operators act on the same function space as the angular momentum operators.
. The function ψ does not play any role and is dropped from the equation. The rotation operators act on the same function space as the angular momentum operators.
[edit] One-dimensional application
Let us consider the case β = γ = 0, so that the only rotation is around the z-axis over an angle α(t). This gives from the previous result,
The chain rule gives
Hence,
Remember that
and that for rotations around one fixed axis it holds that
Then multiplying left and right-hand side:
Since the rotation around z commutes with 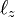 the order of the factors on the right hand side is free. We arrive at the differential equation
the order of the factors on the right hand side is free. We arrive at the differential equation
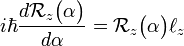 .
.
Integration gives
This is a well-known and often used expression for a rotation operator in terms of the orbital-angular momentum operator.
Consider an infinitesimal rotation Δα, that is, (Δα)² << Δα then expansion of the exponent can be truncated after two terms
This equation is the source of the often found statement that the component of an orbital-angular momentum is the generator of an infinitesimal rotation.
[edit] Notes
- ↑ A. Messiah, Quantum Mechanics, North Holland, Amsterdam (1967) Chapter VII
- ↑ A matrix M = (Mi,j) is antisymmetric if Mi,j = −Mj,i for all i and j.
- ↑ W. Miller, Jr. Symmetry Groups and their Applications, Academic Press, Vol. 50 in Pure and Applied Mathematics, New York (1972), p. 189


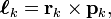
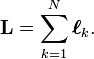
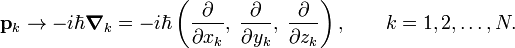
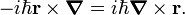
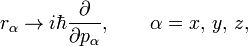
![[A,B] := AB - BA \;.](../w/images/math/5/e/3/5e332d8e634a3225e6fb2f069f80f8fc.png)
![[L_x, \, L_y] = i\hbar L_z,\quad [L_z, \, L_x]= i\hbar L_y,\quad [L_y, \, L_z] = i\hbar L_x.](../w/images/math/7/9/2/79239fbe386b8127382a6ff523f3274f.png)
![[H, L_\alpha] = 0, \quad \alpha=x,y,z.](../w/images/math/3/c/f/3cf357c9d1ec468e7e9b5e3ddab9b5e0.png)
![[[A,B],C] + [[B,C],A]+[[C,A]],B] = 0 \; ,](../w/images/math/5/1/0/5105fb77c7d72a6e26c31170d0810598.png)
![\left.
\begin{matrix}
[AB, C] &= A[B,C] + [A,C]B \\
-[BA, C] &= - [B,C]A -B[A, C] \\
\end{matrix}
\right\}\; \Longrightarrow\; [[A,B],C] = [A, [B,C]] + [[A,C],B].](../w/images/math/3/e/1/3e1bf96a0f2bcf0e11c3bb7b689723e9.png)
![[[A,B],C] \ne [A, [B,C]] \quad\hbox{because in general}\quad [[A,C],B]\ne 0.](../w/images/math/d/6/7/d670d2e1b01f90efe12dbfe4e4aeb81f.png)
![[A,B] = -[B,A],\quad\hbox{and}\quad [c_1 A+ c_2 B, C] = c_1[A,C] + c_2[B,C]](../w/images/math/8/d/5/8d5818f5ef2d077bb9019159ade7c7cd.png)
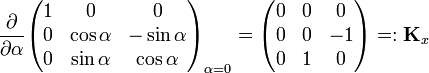
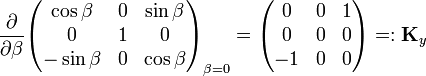
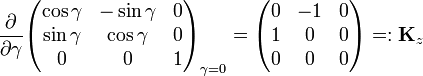

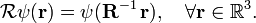
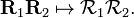
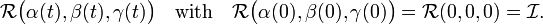
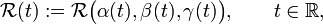
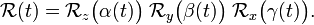
![\left[ \frac{d \mathcal{R}(t) \psi(\mathbf{r} ) } {dt} \right]_{t=0} =
\left[ \frac{d \psi(\mathbf{R}(t)^{-1}\mathbf{r} ) } {dt} \right]_{t=0}\quad\hbox{with}\quad
\mathbf{R}(t) = \mathbf{R}_z\big(\alpha(t)\big)\;
\mathbf{R}_y\big(\beta(t)\big)\; \mathbf{R}_x\big(\gamma(t)\big).](../w/images/math/a/4/e/a4eba0152157957736a3cd159644f755.png)
![\left[ \frac{d \mathcal{R}(t) \psi(\mathbf{r} ) } {dt} \right]_{t=0} =
\left[ \frac{d \psi(\mathbf{s}(t) ) } {dt} \right]_{t=0}
= \sum_{i=1}^3 \frac{\partial \psi(\mathbf{r}) } {\partial r_i} \left[ \frac{d s_i(t)}{dt} \right]_{t=0} = \boldsymbol{\nabla}\psi \cdot \left[ \dot{\mathbf{s}} \right]_{t=0},
\qquad\qquad\qquad\qquad\qquad (1)](../w/images/math/3/5/a/35a298e271aea801bbd15163489a7b59.png)
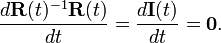
![\left[\frac{d\mathbf{R}(t)^{-1}\mathbf{R}(t)}{dt}\right]_{t=0} =
\left[\frac{d\mathbf{R}(t)^{-1}}{dt}\right]_{t=0}
+\left[\frac{d\mathbf{R}(t)}{dt}\right]_{t=0} = \mathbf{0},](../w/images/math/4/a/c/4ac3924a2d7119fd8e2e3a820f40a797.png)
![\left[\frac{d\mathbf{R}(t)^{-1}}{dt}\right]_{t=0} = - \left[\frac{d\mathbf{R}(t)}{dt}\right]_{t=0}.](../w/images/math/a/d/8/ad815c8e74401968fab7a2da1a44c723.png)
![\begin{align}
\left[\dot{\mathbf{s}}\right]_{t=0} &=
\left[ \frac{d \mathbf{R}^{-1}}{dt}\right]_{t=0} \; \mathbf{r} \\
&= - \left[
\frac{d\mathbf{R}_z(\alpha(t))}{dt}\mathbf{R}_y(\beta(t))\mathbf{R}_x(\gamma(t))
+ \mathbf{R}_z(\alpha(t))\frac{d\mathbf{R}_y(\beta(t))}{dt}\mathbf{R}_x(\gamma(t))
+ \mathbf{R}_z(\alpha(t))\mathbf{R}_y(\beta(t))\frac{d\mathbf{R}_x(\gamma(t))}{dt}
\right]_{t=0}\,\mathbf{r} \\
&=- \left[\frac{d\mathbf{R}_z(\alpha(t))}{dt} + \frac{d\mathbf{R}_y(\beta(t))}{dt}+\frac{d\mathbf{R}_x(\gamma(t))}{dt}\right]_{t=0}\,\mathbf{r}\\
\end{align}](../w/images/math/d/e/7/de786acb1272fef14495fd3f5986ac47.png)
![\left[\frac{d\mathbf{R}_z(\alpha(t))}{dt}\right]_{t=0} = \left[\frac{\partial \mathbf{R}_z(\alpha(t))}{\partial \alpha}\right]_{\alpha = 0}
\left[\frac{d \alpha}{dt}\right]_{t=0} = \mathbf{K}_z \; \dot{\alpha}(0),](../w/images/math/c/a/e/cae0851e60d36843be0cf98c12de52a2.png)
![\big[ \dot{\mathbf{s}}\big]_{t=0}
= - \left[\mathbf{K}_x\; \omega_x + \mathbf{K}_y\; \omega_y + \mathbf{K}_z\; \omega_z\right] \; \mathbf{r}](../w/images/math/1/2/e/12e310203b8b090ce3f925ab604dab14.png)
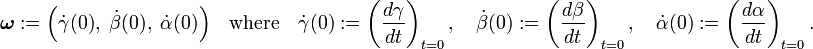
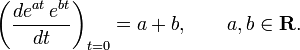
![\big[ \dot{\mathbf{s}}\big]_{t=0} =
-
\begin{pmatrix}
0 & -\omega_z & \omega_y \\
\omega_z & 0 & -\omega_x \\
-\omega_y & \omega_x & 0 \\
\end{pmatrix}
\begin{pmatrix}
x \\
y\\
z\\
\end{pmatrix}
=-\begin{pmatrix}
-\omega_z y + \omega_y z \\
\omega_z x - \omega_x z\\
-\omega_y x + \omega_x z\\
\end{pmatrix}
=
-\boldsymbol{\omega}\times \mathbf{r},](../w/images/math/6/2/0/62068c33a1b6f2981b54741006d72d92.png)
![\left[ \frac{d \mathcal{R}(t) \psi(\mathbf{r} ) } {dt} \right]_{t=0}
=\left[ \frac{d \psi( \mathbf{s}(t) ) }{dt}\right]_{t=0} =
- \big(\boldsymbol{\omega}\times \mathbf{r}\big)\cdot \boldsymbol{\nabla}\psi = -\boldsymbol{\omega} \cdot \big(\mathbf{r}\times\boldsymbol{\nabla} \psi(\mathbf{r})\big),](../w/images/math/f/e/2/fe21a8b70d546077888161f912836413.png)
![\mathcal{L}_{\boldsymbol{\omega}} \psi := \left[ \frac{d \psi(\mathbf{R}(t)^{-1} \mathbf{r} ) }{dt}\right]_{t=0}, \qquad \mathbf{R}(t) \in \mathrm{SO(3)},](../w/images/math/d/8/0/d80dace56a26b4092059687ff1096c57.png)
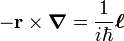
![i\hbar\mathcal{L}_\boldsymbol{\omega}= i\hbar \left[ \frac{d \mathcal{R}_z\big(\alpha(t)\big)\;\mathcal{R}_y\big(\beta(t)\big)\;\mathcal{R}_x\big(\gamma(t)\big) } {dt} \right]_{t=0}
= \Big( \omega_z \ell_z
+ \omega_y \ell_y
+ \omega_z \ell_x\Big)=
\Big( \dot{\alpha}(0) \ell_z
+\dot{\beta}(0) \ell_y
+\dot{\gamma}(0) \ell_x\Big)](../w/images/math/e/c/7/ec7b3811e4ab1fe92443bcc1450c6a98.png)
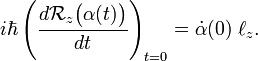
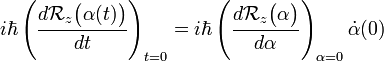
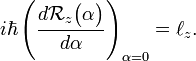
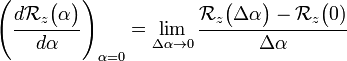
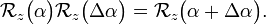
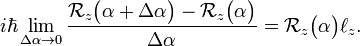
![\mathcal{R}_z\big(\alpha\big) = \exp\left[-i \alpha \ell_z/\hbar\right].](../w/images/math/8/b/e/8bee95ef29cb2b2d9c35888bede4544d.png)