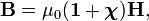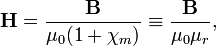Magnetic field
In physics, a magnetic field (commonly denoted by H and sometimes referred to as magnetic intensity) describes a magnetic force (a vector) on a magnetic probe (for instance a piece of iron) at every point in space; it is a vector field. In non-relativistic physics, the space in question is the three-dimensional Euclidean space 𝔼3—the infinite world that we live in.
In general H is seen as an auxiliary field useful when a magnetizable medium is present. The magnetic flux density B is usually seen as the fundamental magnetic field, see the article about B for more details about magnetism.
The SI unit of magnetic field strength is ampere⋅turn/meter; a unit that is based on the magnetic field of a solenoid. In the Gaussian system of units |H| has the unit oersted, with one oersted being equivalent to (1000/4π)⋅A⋅turn/m.
[edit] Relation between H and B
The magnetic field H is closely related to the magnetic induction B (also a vector field). It is the vector B that gives the magnetic force on moving charges (Lorentz force). Historically, the theory of magnetism developed from Coulomb's law, where H played a pivotal role and B was an auxiliary field, which explains its historic name "magnetic induction". At present the roles have swapped and some authors give B the name magnetic field (and do not give a name to H other than "auxiliary field").
The relation between B and H is for the most common case of linear materials[1] in SI units,
where 1 is the 3×3 unit matrix, χ the magnetic susceptibility tensor of the magnetizable medium, and μ0 the magnetic permeability of the vacuum (also known as magnetic constant). In Gaussian units the relation is
Most non-ferromagnetic materials are linear and isotropic; in the isotropic case the susceptibility tensor is equal to χm1, and H can easily be solved (in SI units)
with the relative magnetic permeability μr = 1 + χm.
For example, at standard temperature and pressure (STP) air, a mixture of paramagnetic oxygen and diamagnetic nitrogen, is paramagnetic (i.e., has positive χm), the χm of air is 4⋅10−7. Argon at STP is diamagnetic with χm = −1⋅10−8. For most ferromagnetic materials χm depends on H, with a non-linear relation between H and B and is large (depending on the material) from, say, 50 to 10000 and strongly varying as a function of H.
Both magnetic fields, H and B, are solenoidal (divergence-free, transverse) vector fields because of one of Maxwell's equations
This equation denies the existence of magnetic monopoles (magnetic charges) and hence also of magnetic currents.
[edit] Note
- ↑ For non-linear materials, or very strong fields, second and higher powers of H appear in the relation between B and H.