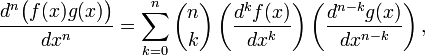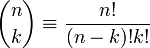Leibniz rule

From Knowino
Jump to: navigation, search

In mathematics, the Leibniz rule is a rule for applying the nth power of a differential operator to a product function (differentiating n times the product function).

Let f(x) and g(x) be n times differentiable functions of x. Then Leibniz's rule states the following

\frac{d^n \big(f(x) g(x)\big)}{dx^n} = \sum_{k=0}^n \binom{n}{k} \left(\frac{d^k f(x)}{dx^k}\right)\left( \frac{d^{n-k} g(x)}{dx^{n-k}}\right),

where

\binom{n}{k} \equiv \frac{n!}{(n-k)!k!}

is a binomial coefficient.

Retrieved from "http://knowino.org/wiki/Leibniz_rule"
Personal tools
Variants
Actions
Navigation
Community
Toolbox