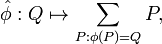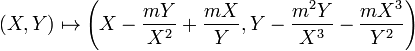Isogeny

In algebraic geometry, an isogeny between abelian varieties is a rational map which is also a group homomorphism, with finite kernel.

Contents 1 Elliptic curves 1.1 Examples 1.1.1 Degree 2 1.1.2 Degree 3 1.2 Elliptic curves over the complex numbers 1.3 Elliptic curves over finite fields 2 References

[edit] Elliptic curves

As 1-dimensional abelian varieties, elliptic curves provide a convenient introduction to the theory. If 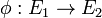is a non-trivial rational map which maps the zero of E₁ to the zero of E₁, then it is necessarily a group homomorphism. The kernel of φ is a proper subvariety of E₁ and hence a finite set of order d, the degree of φ. Conversely, every finite subgroup of E₁ is the kernel of some isogeny.

There is a dual isogeny 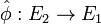defined by

the sum being taken on E₁ of the d points on the fibre over Q. This is indeed an isogeny, and the composite 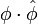is just multiplication by d.

The curves E₁ and E₂ are said to be isogenous: this is an equivalence relation on isomorphism classes of elliptic curves.

[edit] Examples

Let E₁ be an elliptic curve over a field K of characteristic not 2 or 3 in Weierstrass form.

[edit] Degree 2

A subgroup of order 2 on E₁ must be of the form 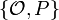where P = (e,0) with e being a root of the cubic in X. Translating so that e=0 and the curve has equation Y² = X³ + AX² + BX, the map

is an isogeny from E₁ to the isogenous curve E₂ with equation Y² = X³ − 2AX² + (A² − 4B)X.

[edit] Degree 3

A subgroup of order 3 must be of the form where x is in K but y need not be. We shall assume that 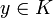(by taking a quadratic twist if necessary). Translating, we can put E in the form Y² + XY + mY = X³. The map

is an isogeny from E₁ to the isogenous curve E₂ with equation Y² + XY + 3mY = X³ − 6mX − (m + 9m²).

[edit] Elliptic curves over the complex numbers

An elliptic curve over the complex numbers is isomorphic to a quotient of the complex numbers by some lattice. If E₁ = C/L₁, and L₁ is a sublattice of L₂ of index d, then E₂ = C/L₂ is an isogenous curve. Representing the homothety class of a lattice by a point τ in the upper half-plane, the isogenous curves correspond to the lattices with moduli

with a.c = d and b=0,1,...,c-1.

[edit] Elliptic curves over finite fields

Isogenous elliptic curves over a finite field have the same number of points (although not necessarily the same group structure). The converse is also true: this is the Honda-Tate theorem.

[edit] References

• J.W.S. Cassels (1991). Lectures on Elliptic Curves. Cambridge University Press, 58-65. ISBN 0-521-42530-1. 
• Dale Husemöller (1987). Elliptic curves. Springer-Verlag, 91-96,163. ISBN 0-387-96371-5. 
• Joseph H. Silverman (1986). The Arithmetic of Elliptic Curves. Springer-Verlag, 70-79,84-90. ISBN 0-387-96203-4. 

Some content on this page may previously have appeared on Citizendium.