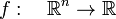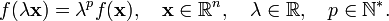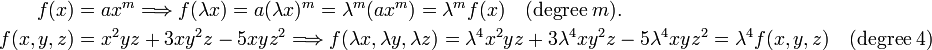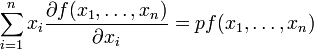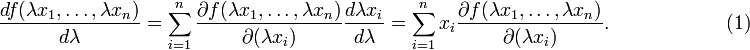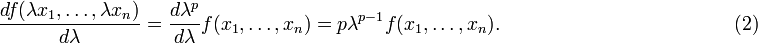Homogeneous function
From Knowino
In mathematics, a function f,
is homogeneous of degree p, if
The degree of homogeneity p is a positive integral number.
[edit] Examples
[edit] Euler's theorem
Let f be differentiable and homogeneous of order p, then
[edit] Proof
By the chain rule
From the homogeneity,
Compare Eqs (1) and (2) for λ = 1 and the result to be proved follows.