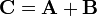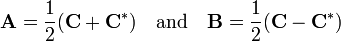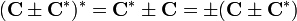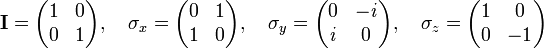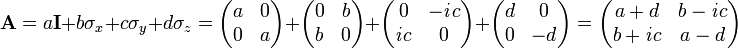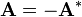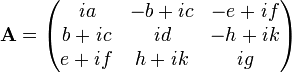Hermitian matrix
A Hermitian matrix (or self-adjoint matrix) is one which is equal to its Hermitian adjoint (also known as its conjugate transpose). Every entry in the transposed matrix is equal to the complex conjugate of the corresponding entry in the original matrix:
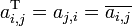 ,
,
or in matrix notation:
 ,
,
where AT stands for A transposed. In physics the dagger symbol is often used instead of the star:
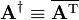 ,
,
so that a physics text would define a Hermitian matrix as a matrix satisfying
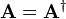 .
.
Contents |
[edit] Forming the Hermitian adjoint
As an example a general 3×3 Hermitian matrix is introduced:
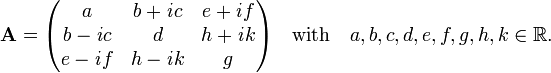 .
.
First we form the transpose matrix by replacing Ai,j with Aj,i,
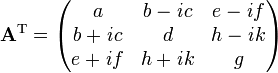 .
.
Second, we take the complex conjugate of each entry to form the Hermitian adjoint:
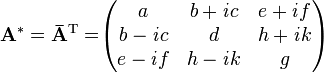 .
.
We find that
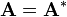 .
.
In the example just given we see that 9 real numbers determine the 3×3 Hermitian matrix completely. This is an example of a general result: an n×n Hermitian matrix is determined by n2 real parameters.
The proof is by counting. An n×n general complex matrix has n2 matrix elements and every element is specified by two real numbers (the real and imaginary part of the complex matrix element). Hermiticity gives n2 conditions, so the number of real degrees of freedom is 2n2−n2 = n2. The n2 Hermiticiy conditions are the following: Imaginary parts of diagonal elements are zero (n conditions). Real parts of matrix elements below the diagonal are equal to those above the diagonal. Since there are ½ n(n−1) elements below the diagonal, this gives that many conditions. Another ½ n(n−1) conditions is delivered by the fact that the imaginary parts of the corresponding elements below and above the diagonal have opposite signs and are of equal absolute value. Hence, in total there are
- n + ½ n(n−1) + ½ n(n−1) = n2
conditions.
[edit] Properties
[edit] Entries on the main diagonal
It may be seen that all entries on the main diagonal of a Hermitian matrix must be real. Indeed, by definition 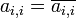 which implies
which implies 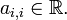
[edit] Real-valued Hermitian matrices
A real-valued Hermitian matrix is a real symmetric matrix and hence the theorems of the latter are special cases of theorems of the former.
[edit] Decomposition
Any square matrix C can be written as the sum of a Hermitian matrix A and skew-Hermitian matrix (see below) B:
where
It follows immediately from the linearity of the Hermitian adjoint that A is Hermitian and B skew-Hermitian:
[edit] Normal
All Hermitian matrices are normal, i.e.  , and thus the finite dimensional spectral theorem applies. This means that any Hermitian matrix can be diagonalised by a unitary matrix, all its entries have real values
, and thus the finite dimensional spectral theorem applies. This means that any Hermitian matrix can be diagonalised by a unitary matrix, all its entries have real values
[edit] Eigenvalues
All the eigenvalues of Hermitian matrices are real. Eigenvectors with distinct eigenvalues are orthogonal.
[edit] Pauli spin matrices
Any 2x2 Hermitian matrix may be written as a linear combination of the 2×2 identity matrix and the three Pauli spin matrices. These matrices have use in quantum mechanics. The four matrices form an orthogonal basis for the 4-dimensional vector space of 2x2 Hermitian matrices.
An arbitrary 2×2 Hermitian matrix A is written thus,
[edit] Skew-Hermitian Matrices
A skew-Hermitian matrix is one which is equal to the negative of its Hermitian adjoint:
For instance, (a, b, c, d, e, f, g, h, and k are real),
is a skew-Hermitian matrix. Clearly, the entries on the main diagonal are purely imaginary.
[edit] References
Matrices and Determinants, 9th edition by A.C Aitken
[edit] See Also
| |
Some content on this page may previously have appeared on Citizendium. |