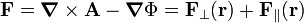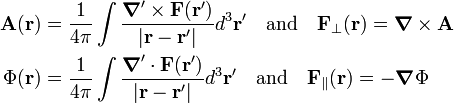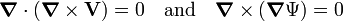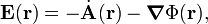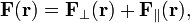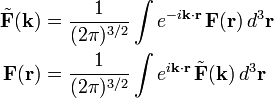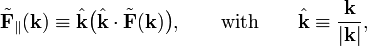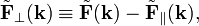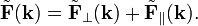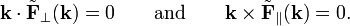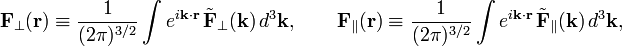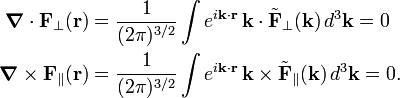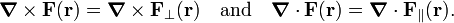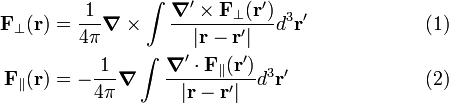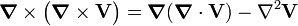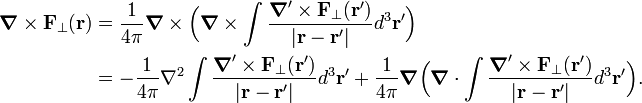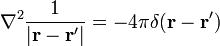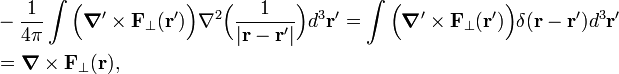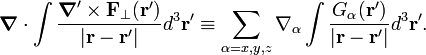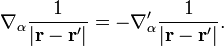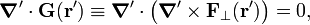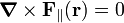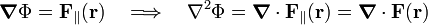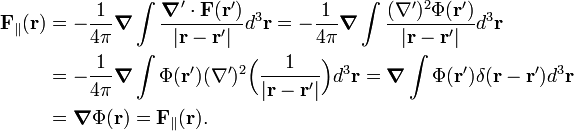Helmholtz decomposition

From Knowino
Jump to: navigation, search

In vector analysis, the Helmholtz decomposition of a vector field on 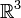\mathbb{R}^3 is the decomposition of the vector field into two vector fields, one a divergence-free field and one a curl-free field. The decomposition is called after the German physiologist and physicist Hermann von Helmholtz (1821 – 1894).

Contents

[edit] Mathematical formulation

The Helmholtz decomposition may be formulated as follows. Any vector field F(r) that is sufficiently often differentiable and vanishes sufficiently fast at infinity can be written as,

\mathbf{F} = \boldsymbol{\nabla}\times \mathbf{A} -\boldsymbol{\nabla}\Phi = \mathbf{F}_\perp(\mathbf{r})+\mathbf{F}_\parallel(\mathbf{r})

with

\begin{align} \mathbf{A}(\mathbf{r}) &= \frac{1}{4\pi} \int \frac{\boldsymbol{\nabla}'\times \mathbf{F}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \quad\hbox{and}\quad \mathbf{F}_\perp(\mathbf{r}) = \boldsymbol{\nabla}\times \mathbf{A}\\ \Phi(\mathbf{r}) & = \frac{1}{4\pi} \int \frac{\boldsymbol{\nabla}'\cdot \mathbf{F}(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \quad\hbox{and}\quad \mathbf{F}_\parallel(\mathbf{r}) = -\boldsymbol{\nabla}\Phi \\ \end{align}

The primed nabla operator ∇' acts on primed coordinates and the unprimed ∇ acts on unprimed coordinates.

Note that

\boldsymbol{\nabla}\cdot(\boldsymbol{\nabla} \times \mathbf{V}) = 0\quad\hbox{and}\quad \boldsymbol{\nabla}\times (\boldsymbol{\nabla} \Psi) = 0

holds for any vector field V(r) and any scalar function Ψ(r). Hence it follows that the first term of F is divergence-free and the second curl-free.

As a corollary follows that the specification of both the divergence and the curl of a vector field at all points of space gives the field uniquely.

A well-known example of a Helmholtz decomposition is the following form of the electric field E,

\mathbf{E}(\mathbf{r}) = -\dot{\mathbf{A}}(\mathbf{r}) -\boldsymbol{\nabla}\Phi(\mathbf{r}),

where Φ is the electric potential and A is the (magnetic) vector potential. The dot indicates a derivative with respect to time.

[edit] Decomposition in transverse and longitudinal components

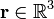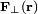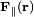Above it was stated that a vector field F(r) with \mathbf{r} \in \mathbb{R}^3 can be decomposed in a transverse \scriptstyle\mathbf{F}_\perp(\mathbf{r}) and longitudinal component \scriptstyle\mathbf{F}_\parallel(\mathbf{r}):

\mathbf{F}(\mathbf{r}) = \mathbf{F}_\perp(\mathbf{r})+\mathbf{F}_\parallel(\mathbf{r}),

where

\boldsymbol{\nabla}\cdot \mathbf{F}_\perp(\mathbf{r}) = 0,\qquad \boldsymbol{\nabla}\times \mathbf{F}_\parallel(\mathbf{r}) = \mathbf{0}.

Thus, an arbitrary field F(r) can be decomposed in a part that is divergence-free, the transverse component, and a part that is curl-free, the longitudinal component. This will now be proved directly, without making the detour via the integral expressions for A(r) and Φ(r).

[edit] Proof of decomposition

The decomposition is formulated in r-space. By a Fourier transform the decomposition may be formulated in k-space. This is advantageous because differentiations in r-space become multiplications in k-space. We will show that divergence in r-space becomes an inner product in k-space and a curl becomes a cross product. Thus, we define the mutually inverse Fourier transforms,

\begin{align} \tilde{\mathbf{F}}(\mathbf{k}) & = \frac{1}{ (2\pi)^{3/2} }\int e^{-i\mathbf{k}\cdot\mathbf{r}}\, \mathbf{F}(\mathbf{r})\, d^3\mathbf{r} \\ \mathbf{F}(\mathbf{r}) & = \frac{1}{ (2\pi)^{3/2} }\int e^{i\mathbf{k}\cdot\mathbf{r}} \,\tilde{\mathbf{F}}(\mathbf{k})\, d^3\mathbf{r} \\ \end{align}

An arbitrary vector field in k-space can be decomposed in components parallel and perpendicular to k,

\tilde{\mathbf{F}}_\parallel (\mathbf{k}) \equiv \hat{\mathbf{k}} \big(\hat{\mathbf{k}}\cdot \tilde{\mathbf{F}}(\mathbf{k})\big), \qquad\hbox{with}\qquad \hat{\mathbf{k}} \equiv \frac{\mathbf{k}}{|\mathbf{k}|},
\tilde{\mathbf{F}}_\perp (\mathbf{k}) \equiv \tilde{\mathbf{F}}(\mathbf{k}) -\tilde{\mathbf{F}}_\parallel(\mathbf{k}),

so that

\tilde{\mathbf{F}} (\mathbf{k}) = \tilde{\mathbf{F}}_\perp (\mathbf{k}) + \tilde{\mathbf{F}}_\parallel (\mathbf{k}).

Clearly,

\mathbf{k}\cdot \tilde{\mathbf{F}}_\perp (\mathbf{k}) = 0 \qquad\hbox{and}\qquad \mathbf{k}\times \tilde{\mathbf{F}}_\parallel (\mathbf{k}) = 0.

Transforming back, we get

\mathbf{F}_\perp(\mathbf{r}) \equiv \frac{1}{ (2\pi)^{3/2} }\int e^{i\mathbf{k}\cdot\mathbf{r}}\, \tilde{\mathbf{F}}_\perp(\mathbf{k})\, d^3\mathbf{k}, \qquad \mathbf{F}_\parallel(\mathbf{r}) \equiv \frac{1}{ (2\pi)^{3/2} }\int e^{i\mathbf{k}\cdot\mathbf{r}}\, \tilde{\mathbf{F}}_\parallel(\mathbf{k})\, d^3\mathbf{k},

which satisfy the properties

\begin{align} \boldsymbol{\nabla}\cdot \mathbf{F}_\perp(\mathbf{r}) &= \frac{1}{ (2\pi)^{3/2} }\int e^{i\mathbf{k}\cdot\mathbf{r}}\, \mathbf{k}\cdot\tilde{\mathbf{F}}_\perp(\mathbf{k})\, d^3\mathbf{k} = 0 \\ \boldsymbol{\nabla}\times \mathbf{F}_\parallel(\mathbf{r}) &= \frac{1}{ (2\pi)^{3/2} }\int e^{i\mathbf{k}\cdot\mathbf{r}}\, \mathbf{k}\times\tilde{\mathbf{F}}_\parallel(\mathbf{k})\, d^3\mathbf{k} = 0. \end{align}

Hence we have found the required decomposition.

[edit] Integral expressions for the transverse and longitudinal components

The curl and the divergence of the vector field F(r) satisfy,

\boldsymbol{\nabla} \times \mathbf{F}(\mathbf{r}) = \boldsymbol{\nabla} \times \mathbf{F}_\perp(\mathbf{r})\quad\hbox{and}\quad\boldsymbol{\nabla} \cdot \mathbf{F}(\mathbf{r}) = \boldsymbol{\nabla} \cdot \mathbf{F}_\parallel(\mathbf{r}).

Using this, we see that the following relations were stated earlier in fact:

\begin{align} \mathbf{F}_\perp(\mathbf{r}) &= \frac{1}{4\pi}\boldsymbol{\nabla} \times \int \frac{\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \qquad\qquad \qquad (1)\\ \mathbf{F}_\parallel(\mathbf{r}) &= -\frac{1}{4\pi}\boldsymbol{\nabla} \int \frac{\boldsymbol{\nabla}'\cdot \mathbf{F}_\parallel(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \qquad\qquad\qquad \quad (2)\\ \end{align}

They are, respectively, the perpendicular (transverse, divergence-free) and parallel (longitudinal, curl-free) components of the field F(r). We reiterate that the operator ∇ acts on unprimed coordinates and ∇' on primed coordinates. Note that the two components of F(r) are uniquely determined once the curl and the divergence of F(r) are known. The integral relations will now be proved.

[edit] Proof of integral expressions

We will confirm the integral forms, equations (1) and (2), of the components. They will be shown to lead to identities.

[edit] Transverse component

For the perpendicular (transverse) component we note that for any vector V,

\boldsymbol{\nabla} \times \big( \boldsymbol{\nabla} \times \mathbf{V} \big)= \boldsymbol{\nabla} (\boldsymbol{\nabla} \cdot \mathbf{V}) - \nabla^2 \mathbf{V}

and insert this in

\begin{align} \boldsymbol{\nabla} \times\mathbf{F}_\perp(\mathbf{r}) &= \frac{1}{4\pi}\boldsymbol{\nabla} \times\Big(\boldsymbol{\nabla} \times \int \frac{\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \Big) \\ &= -\frac{1}{4\pi} \nabla^2\int \frac{\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' + \frac{1}{4\pi}\boldsymbol{\nabla} \Big(\boldsymbol{\nabla} \cdot \int \frac{\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \Big). \end{align}

Below we will show that second term vanishes. Use for the first term the following equation for the Dirac delta function,

\nabla^2 \frac{1}{|\mathbf{r}-\mathbf{r}'|} = -4\pi \delta(\mathbf{r}-\mathbf{r}')

Hence the first term becomes (note that the unprimed nabla may be moved under the integral)

\begin{align} &-\frac{1}{4\pi}\int \Big(\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}')\Big) \nabla^2 \Big( \frac{1}{|\mathbf{r}-\mathbf{r}'|} \Big) d^3\mathbf{r}' = \int \Big(\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}') \Big) \delta(\mathbf{r}-\mathbf{r}') d^3\mathbf{r}' \\ &= \boldsymbol{\nabla}\times \mathbf{F}_\perp(\mathbf{r}), \end{align}

so that we indeed end up with an identity.

Before turning to the parallel (longitudinal) term we prove that the second term vanishes. To that end we introduce a shorthand notation

\boldsymbol{\nabla}\cdot \int \frac{\boldsymbol{\nabla}'\times \mathbf{F}_\perp(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' \equiv \sum_{\alpha=x,y,z} \nabla_\alpha \int \frac{G_\alpha(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r}' .

Move the divergence under the integral and use

\nabla_\alpha \frac{1}{|\mathbf{r}-\mathbf{r}'|} = - \nabla_\alpha' \frac{1}{|\mathbf{r}-\mathbf{r}'|} .

By partial integration and using that the integrand vanishes for the integral limits, we can let −∇'α act on Gα(r' ) (this trick is known as the turnover rule for the anti Hermitian operator ∇'α). Then from

\boldsymbol{\nabla}' \cdot \mathbf{G}(\mathbf{r}') \equiv \boldsymbol{\nabla}' \cdot \big(\boldsymbol{\nabla}' \times \mathbf{F}_\perp(\mathbf{r}')\big) = 0,

(because the divergence of the curl of any vector is zero) follows the vanishing of the second term.

[edit] Longitudinal component

From

\boldsymbol{\nabla} \times \mathbf{F}_\parallel(\mathbf{r}) = 0

follows that there is a scalar function Φ such that

\boldsymbol{\nabla}\Phi = \mathbf{F}_\parallel(\mathbf{r}) \quad\Longrightarrow\quad \nabla^2 \Phi = \boldsymbol{\nabla}\cdot \mathbf{F}_\parallel(\mathbf{r}) = \boldsymbol{\nabla}\cdot \mathbf{F}(\mathbf{r})

We work toward an identity, using the turnover rule for the Laplace operator ∇2, which may be proved by partial integration and the assumption that the integrand vanishes at the integration limits,

\begin{align} \mathbf{F}_\parallel(\mathbf{r}) &= -\frac{1}{4\pi}\boldsymbol{\nabla}\int \frac{\boldsymbol{\nabla}'\cdot \mathbf{F}(\mathbf{r}') }{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r} = -\frac{1}{4\pi}\boldsymbol{\nabla}\int \frac{(\nabla')^2 \Phi(\mathbf{r'})}{|\mathbf{r}-\mathbf{r}'|} d^3\mathbf{r} \\ &= -\frac{1}{4\pi}\boldsymbol{\nabla}\int \Phi(\mathbf{r'})(\nabla')^2 \Big( \frac{1} {|\mathbf{r}-\mathbf{r}'|}\Big) d^3\mathbf{r} = \boldsymbol{\nabla}\int \Phi(\mathbf{r'}) \delta(\mathbf{r}-\mathbf{r}') d^3\mathbf{r} \\ &= \boldsymbol{\nabla} \Phi(\mathbf{r}) = \mathbf{F}_\parallel(\mathbf{r}). \end{align}
Retrieved from "http://knowino.org/wiki/Helmholtz_decomposition"
Personal tools
Variants
Actions
Navigation
Community
Toolbox