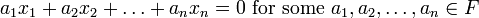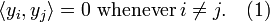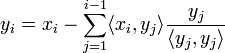Gram-Schmidt orthogonalization

From Knowino
Jump to: navigation, search

In mathematics, especially in linear algebra, Gram-Schmidt orthogonalization is a sequential procedure or algorithm for constructing a set of mutually orthogonal vectors from a given set of linearly independent vectors. Orthogonalization is important in diverse applications in mathematics and the applied sciences because it can often simplifiy calculations or computations by making it possible, for instance, to do the calculation in a recursive manner.

[edit] The Gram-Schmidt orthogonalization algorithm

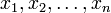Let X be an inner product space over the sub-field F of real or complex numbers with inner product \langle \cdot,\cdot \rangle, and let x_1,x_2,\ldots,x_n be a collection of linearly independent elements of X. Recall that linear independence means that

a_1 x_1 + a_2 x_2 + \ldots + a_n x_n=0 {\,\,\rm for\,\,some\,\,} a_1,a_2,\ldots,a_n \in F

implies that 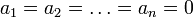a_1=a_2=\ldots=a_n=0. The Gram-Schmidt orthogonalization procedure constructs, in a sequential manner, a new sequence of vectors 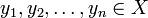y_1,y_2,\ldots,y_n \in X such that:

\langle y_i,y_j \rangle = 0 \,\, {\rm whenever\,} i \neq j. \quad (1)

The vectors 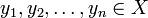y_1,y_2,\ldots,y_n \in X satisfying (1) are said to be orthogonal.

The Gram-Schmidt orthogonalization algorithm is actually quite simple and goes as follows:

Set y1 = x1
For i = 2 to n,
y_i=x_i - \sum_{j=1}^{i-1}\langle x_i,y_{j} \rangle \frac{y_{j}}{\langle y_{j},y_{j}\rangle}
End

It can easily be checked that the sequence 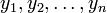y_1,y_2,\ldots,y_n constructed in such a way will satisfy the requirement (1).


[edit] Further reading

  1. H. Anton and C. Rorres, Elementary Linear Algebra with Applications (9 ed.), Wiley, 2005.
Information.svg Some content on this page may previously have appeared on Citizendium.
Retrieved from "http://knowino.org/wiki/Gram-Schmidt_orthogonalization"
Personal tools
Variants
Actions
Navigation
Community
Toolbox