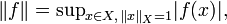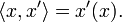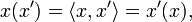Dual space (functional analysis)
In mathematics, particularly in the branch of functional analysis, a dual space refers to the space of all continuous linear functionals on a real or complex Banach space. The dual space of a Banach space is again a Banach space when it is endowed with the operator norm. If X is a Banach space then its dual space is often denoted by X'.
Contents |
[edit] Definition
Let X be a Banach space over a field F which is real or complex, then the dual space X' of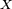 
is the vector space over F of all continuous linear functionals 
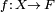when F is endowed with the standard Euclidean topology.
The dual space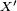 
is again a Banach space when it is endowed with the operator norm. Here the operator norm 
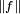of an element 
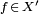is defined as:
where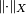 
denotes the norm on X.
[edit] The bidual space and reflexive Banach spaces
Since X' is also a Banach space, one may define the dual space of the dual, often referred to as a bidual space of X and denoted as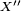 
. There are special Banach spaces X where one has that 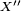coincides with X (i.e., 
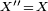), in which case one says that X is a reflexive Banach space (to be more precise, 
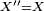here means that every element of 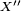corresponds to some element of 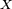as described in the next section).
An important class of reflexive Banach spaces are the Hilbert spaces, i.e., every Hilbert space is a reflexive Banach space. This follows from an important result known as the Riesz representation theorem.
[edit] Dual pairings
If X is a Banach space then one may define a bilinear form or pairing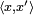 
between any element 
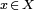and any element 
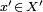defined by
Notice that 
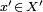defines a continuous linear functional on X for each , while 
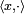defines a continuous linear functional on 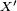for each 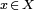. It is often convenient to also express
i.e., a continuous linear functional f on 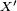is identified as 
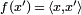for a unique element 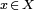. For a reflexive Banach space such bilinear pairings determine all continuous linear functionals on X and 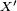since it holds that every functional 
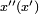with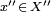 
can be expressed as 
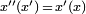for some unique element .
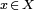Dual pairings play an important role in many branches of mathematics, for example in the duality theory of convex optimization[1].
[edit] References
- ↑ R. T. Rockafellar, Conjugate Duality and Optimization, CBMS Reg. Conf. Ser. Appl. Math. 16, SIAM, Philadelphia, 1974
[edit] Further reading
K. Yosida, Functional Analysis (6 ed.), ser. Classics in Mathematics, Berlin, Heidelberg, New York: Springer-Verlag, 1980
|
Some content on this page may previously have appeared on Citizendium. |
