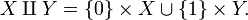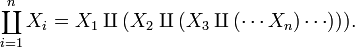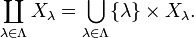Disjoint union
In mathematics, the disjoint union of two sets X and Y is a set which contains disjoint (that is, non-intersecting) "copies" of each of X and Y: it is denoted 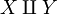 or, less often,
or, less often, 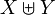 .
.
There are injection maps in1 and in2 from X and Y to the disjoint union, which are injective functions with disjoint images.
If X and Y are disjoint, then the usual union is also a disjoint union. In general, the disjoint union can be realised in a number of ways, for example as
The disjoint union has a universal property: if there is a set Z with maps 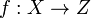 and
and 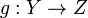 , then there is a map
, then there is a map  such that the compositions
such that the compositions 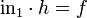 and
and 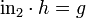 .
.
The disjoint union is commutative, in the sense that there is a natural bijection between 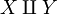 and
and 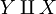 ; it is associative again in the sense that there is a natural bijection between
; it is associative again in the sense that there is a natural bijection between 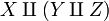 and
and 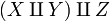 .
.
[edit] General unions
The disjoint union of any finite number of sets may be defined inductively, as
The disjoint union of a general family of sets Xλ as λ ranges over a general index set Λ may be defined as
[edit] References
- Michael D. Potter (1990). Sets: An Introduction. Oxford University Press, 36-37. ISBN 0-19-853399-3.
| |
Some content on this page may previously have appeared on Citizendium. |