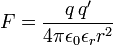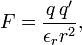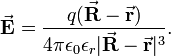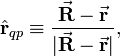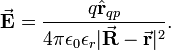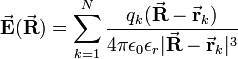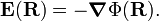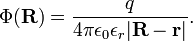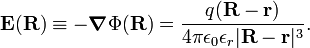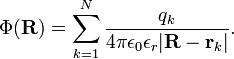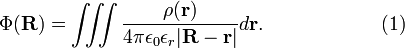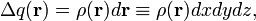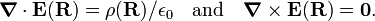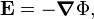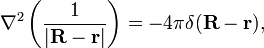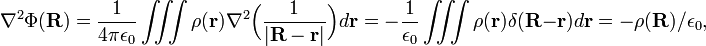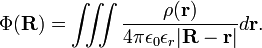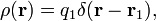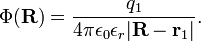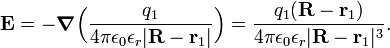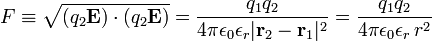Coulomb's law
In physics, Coulomb's law describes the forces acting between electric point charges. The law was first given by Charles-Augustin de Coulomb. It is an inverse-square law for two electric charges very similar to Newton's gravitational law for two masses.
An important difference between Newton's and Coulomb's law is that masses always attract each other, whereas charges may repel or attract. That is, charges may be positive or negative, while masses have the same sign (are always positive by convention). Another important difference is that the gravitational force cannot be weakened by any intervening medium, while Coulomb's law contains a factor (the static relative permittivity εr, also known as dielectric constant) depending on the material that fills the space between the charges. All non-conducting materials (dielectrics) weaken the Coulomb force (have εr > 1).
Contents |
[edit] Formulation
Coulomb discovered experimentally that the force between two small charged bodies separated in air a distance large compared to their dimensions
- varies directly as the magnitude of each charge,
- varies inversely as the square of the distance between them,
- is directed along the line joining the charges,
- is attractive if the bodies are oppositely charged and repulsive if the bodies have the same type of charge.
Further it was shown experimentally that the force is additive, i.e., the force on a test body exerted by a number of charges around it, is the vector sum of the individual two-body forces. Given two charges q and q' a distance r apart, the force F between the particles is in the SI system of units,
The quantities ε0 and εr are the electric constant (also known as vacuum permittivity) and the static relative permittivity (also known as relative dielectric constant) of the medium, respectively. The relative permittivity of air (εr = 1.000536 at ambient temperature and pressure) is so close to the vacuum value (εr = 1) that Coulomb could not have distinguished the difference between charges in air or in vacuum.
In Gaussian units, a non-rationalized system of units, 4π and ε0 are absent, so that the law takes the form
where q and q' are in statC and r is in centimeter. The value of εr is the same as in SI units. In quantum mechanical texts Coulomb's law is often quoted in Gaussian units for the vacuum case, where εr (= 1) is usually dropped from the equation.
[edit] Electrostatic vector field
[edit] Definition electrostatic field
The force 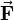 divided by Δq on a test particle of charge Δq is the static electric field
divided by Δq on a test particle of charge Δq is the static electric field 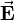 —a vector field. The force originates from one or more charges acting on the test particle. The charge Δq of the test particle is taken infinitesimally small, that is, it is negligible with respect to the charges causing the field and hence the test particle does not influence the electric field.
The direction of the electric field is by convention such that it points away from a positive charge and points toward a negative charge.
—a vector field. The force originates from one or more charges acting on the test particle. The charge Δq of the test particle is taken infinitesimally small, that is, it is negligible with respect to the charges causing the field and hence the test particle does not influence the electric field.
The direction of the electric field is by convention such that it points away from a positive charge and points toward a negative charge.
[edit] Field due to one point charge
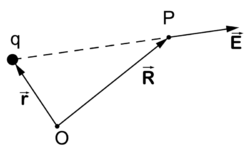
Coulomb's law gives the electric field 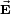 at the point P due to an electrostatic point charge q at position
at the point P due to an electrostatic point charge q at position 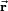 . The strength of the electric field
. The strength of the electric field 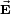 depends on the inverse-squared distance of P to q and is along the line from q to P, that is,
depends on the inverse-squared distance of P to q and is along the line from q to P, that is,
Note that although this may look like an inverse-cubed dependence, we must not forget that the numerator has dimension length. Indeed, defining a (dimensionless) unit vector by
we see more clearly the inverse-squared dependence on distance:
If q is positive the electric field points from q to P, if q is negative it points from P to q. The force on a particle of charge −|Q| is equal to 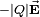 , that is, the force is antiparallel to the vector
, that is, the force is antiparallel to the vector 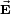 . The force on a particle with charge |Q| is equal to
. The force on a particle with charge |Q| is equal to 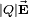 , parallel to the vector
, parallel to the vector 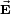 . In total, charges of opposite sign attract and of same sign repel.
. In total, charges of opposite sign attract and of same sign repel.
[edit] Field due to N point charges
The experimentally observed additivity of electrostatic forces gives the following electric field at P when there are N charges qk at fixed positions rk. The electric field is a vector field
depending on 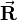 . The sum stands for a vector sum.
. The sum stands for a vector sum.
[edit] Coulomb potential
- From here on we denote vectors by bold letters dropping the arrows on top of the symbols.
When the electrostatic field is irrotational, i.e.,
one can define a potential Φ(r), such that,
Since
it follows that R/R3 is irrotational, and so is (R-r)/|R-r|3. The Coulomb potential Φ exists. The following expression for Φ is consistent with E,
Indeed,
The Coulomb potential is determined up to a constant. By requiring that Φ vanishes for infinite R the constant becomes zero.
The Coulomb potential at the point R due to N charges at rk is
For a continuous charge distribution ρ(r) this expression generalizes to
This generalization follows easily if we first substitute the infinitesimal charge at position r,
and then replace the sum by a volume integral.
[edit] Poisson equation
The Maxwell equations form the postulates of classical electrodynamics. It is of interest to see how the Coulomb potential fits in the postulatory framework devised by James Clerk Maxwell. The following two Maxwell equations are of relevance in the present case in which only static electric charges are considered and there is no magnetic field,
Here we assumed εr = 1 (the vacuum case). The second Maxwell equation tells us that there exists a potential Φ with
so that we obtain
with the Laplace operator ∇2 ≡ ∇⋅∇ (the divergence of the gradient). This equation, which predates Maxwell's equations, was postulated by Siméon Denis Poisson.
In order to show that the Coulomb potential, introduced in Eq. (1) above, satisfies the Poisson equation, we first recall the following result from distribution theory,
where the right hand side is the Dirac delta function. Now, the Laplace operator ∇2 acting on the Coulomb potential of Eq. (1) (with εr = 1) gives
which proves that the Coulomb potential indeed satisfies the Poisson equation. Of course, any function F(R) satisfying the Laplace equation
could have been added to Φ(R) and the result would still be a solution of the Poisson equation. However, physically the presence of F(R) would indicate the presence of charges outside the volume covered by the triple integral. We assume that there are no such charges and hence that F = 0. (This argument can be rephrased as a boundary condition on Φ, we will omit this.)
In summary, the following potential is a solution of the Maxwell equations in the absence of moving charges and a static magnetic field, i.e., of the Poisson equation,
If there is one point charge q1 at position r1, then ρ simplifies to the Dirac delta function,
which yields for the special case of one point charge
From this potential we derive the electric field
The force exerted by this field on a charge q2 at position r2 has strength
which is Coulomb's law in its original formulation, if we remember that r ≡|r2−r1| is the distance between the two charged bodies. We went back in history from two of Maxwell's equations (1864) to the Poisson equation (ca. 1820) and then—for the special of point charges—to Coulomb's equation (1785).
[edit] Reference
J. D. Jackson, Classical Electrodynamics, 2nd edition, John Wiley, New York (1975).