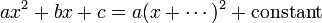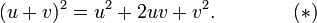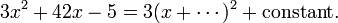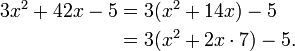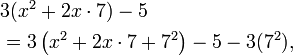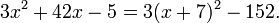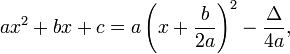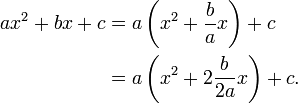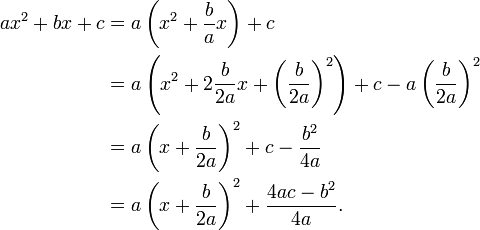Completing the square

From Knowino

Jump to: navigation, search

In algebra, completing the square is a way of rewriting a quadratic polynomial as the sum of a constant and a constant multiple of the square of a first-degree polynomial. Thus one has

$ax^2 + bx + c = a(x+\cdots)^2 + \text{constant}$

and completing the square is the way of filling in the blank between the brackets. Completing the square is used for solving quadratic equations (the proof of the well-known formula for the general solution consists of completing the square). The technique is also used to find the maximum or minimum value of a quadratic function, or in other words, the vertex of a parabola.

The technique relies on the elementary algebraic identity

$(u + v)^2 = u^2 + 2uv + v^2.\qquad\qquad(*)$

[edit] Concrete examples

We want to fill in this blank:

$3x^2 + 42x - 5 = 3(x+\cdots)^2 + \text{constant}.$

We write

$\begin{align} 3x^2 + 42x - 5 & {} = 3(x^2 + 14x) - 5 \\ & {} = 3(x^2 + 2x\cdot 7) - 5. \end{align}$

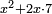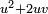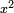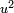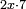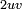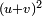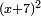Now the expression ( $\scriptstyle x^2 + 2 x \cdot 7$ ) corresponds to $\scriptstyle u^2 + 2 u v$ in the elementary identity labeled (*) above. If $\scriptstyle x^2$ is $\scriptstyle u^2$ and $\scriptstyle 2 x \cdot 7$ is $\scriptstyle 2 u v$ , then $\scriptstyle v$ must be 7. Therefore $\scriptstyle ( u + v )^2$ must be $\scriptstyle ( x + 7 )^2$ . So we continue:

$\begin{align} & {} 3(x^2 + 2x\cdot 7) - 5 \\ & {} = 3\left(x^2 + 2x\cdot 7 + 7^2\right) - 5 - 3(7^2), \end{align}$

Now we have added 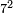$\scriptstyle 7^2$ inside the parentheses, and compensated (thus justifying the "=") by subtracting 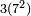$\scriptstyle 3 (7^2)$ outside the parentheses. The expression inside the parentheses is now 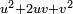$\scriptstyle u^2 + 2 u v + v^2$ , and by the elementary identity labeled (*) above, it is therefore equal to 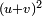$\scriptstyle ( u + v )^2$ , i.e. to 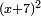$\scriptstyle ( x + 7 )^2$ . So now we have

$3(x + 7)^2 - 5 - 3(7^2) = 3(x + 7)^2 - 152.\,$

Thus we have the equality

$3x^2 + 42x - 5 = 3(x + 7)^2 - 152.\,$

[edit] More abstractly

It is possible to give a closed formula for the completion in terms of the coefficients a, b and c. Namely,

$ax^2+bx + c = a\left(x + \frac{b}{2a}\right)^2 - \frac{\Delta}{4a},$

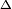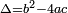where $\scriptstyle \Delta$ stands for the well-known discriminant of the polynomial, that is $\scriptstyle \Delta = b^2 - 4ac$ .

Indeed, we have

$\begin{align} ax^2 + bx + c & {} = a\left( x^2 + \frac{b}{a}x \right) + c \\ & {} = a\left(x^2 + 2\frac{b}{2a}x\right) + c. \end{align}$

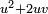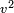The last expression inside parentheses above corresponds to $\scriptstyle u^2 + 2 u v$ in the identity labelled (*) above. We need to add the third term, $\scriptstyle v^2$ :

$\begin{align} ax^2 + bx + c & {} = a\left( x^2 + \frac{b}{a}x \right) + c \\ & {} = a\left(x^2 + 2\frac{b}{2a}x +\left(\frac{b}{2a}\right)^2 \right) + c - a\left(\frac{b}{2a}\right)^2 \\ & {} = a\left(x + \frac{b}{2a}\right)^2 + c - \frac{b^2}{4a} \\ & {} = a\left(x + \frac{b}{2a}\right)^2 + \frac{4ac - b^2}{4a}. \end{align}$

Some content on this page may previously have appeared on Citizendium.

Completing the square

[edit] Concrete examples

[edit] More abstractly

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox