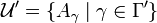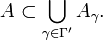Compact space

From Knowino

Jump to: navigation, search

In mathematics, a compact space is a topological space for which every covering of that space by a collection of open sets has a finite subcovering. If the space is a metric space then compactness is equivalent to the space being complete and totally bounded and again equivalent to sequential compactness: that every sequence in this space has a convergent subsequence.

A subset of a topological space is compact if it is compact with respect to the subspace topology. A compact subset of a Hausdorff space is closed, but the converse does not hold in general. For the special case that the set is a subset of a finite dimensional normed space, such as the Euclidean spaces, then compactness is equivalent to that set being closed and bounded: this is the Heine-Borel theorem.

[edit] Cover and subcover of a set

Let A be a subset of a set X. A cover for A is any family of subsets of X whose union contains A. In other words, a cover is of the form

$\mathcal{U}=\{A_{\gamma} \mid \gamma \in \Gamma \}, \quad A_{\gamma} \subset X,$

where $Γ$ is an arbitrary index set, and satisfies

$A \subset \bigcup_{\gamma \in \Gamma }A_{\gamma}.$

An open cover is a cover in which all of the sets $A γ$ are open. Finally, a subcover of 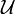$\mathcal{U}$ is a family 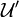$\mathcal{U}'$ of the form

$\mathcal{U}'=\{A_{\gamma} \mid \gamma \in \Gamma'\}$

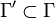with $\Gamma' \subset \Gamma$ such that

$A \subset \bigcup_{\gamma \in \Gamma'}A_{\gamma}.$

[edit] Formal definition of compact space

A topological space X is said to be compact if every open cover of X has a finite subcover, that is, a subcover which contains at most a finite number of subsets of X (in other words, the index set $Γ'$ is finite).

[edit] Finite intersection property

Just as the topology on a topological space may be defined in terms of the closed sets rather than the open sets, so we may transpose the definition of compactness in terms of open sets into a definition in terms of closed sets. A space is compact if the closed sets have the finite intersection property: if 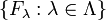$\{ F_\lambda : \lambda \in \Lambda \}$ is a family of closed sets with empty intersection, 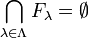$\bigcap_{\lambda \in \Lambda} F_\lambda = \emptyset$ , then there exists a finite subfamily 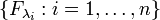$\{ F_{\lambda_i} : i=1,\ldots,n \}$ that has empty intersection, $\bigcap_{i=1}^n F_{\lambda_i} = \emptyset$ .

[edit] Examples

Any finite space.
An indiscrete space.
A space with the cofinite topology.
The Heine-Borel theorem: In Euclidean space with the usual topology, a subset is compact if and only if it is closed and bounded.

[edit] Properties

Compactness is a topological invariant: that is, a topological space homeomorphic to a compact space is again compact.
A closed set in a compact space is again compact.
A subset of a Hausdorff space which is compact (with the subspace topology) is closed.
The quotient topology on an image of a compact space is compact
The image of a compact space under a continuous map is compact.
- A continuous real-valued function on a compact space is bounded and attains its bounds.
The Cartesian product of two (and hence finitely many) compact spaces with the product topology is compact.
The Tychonoff product theorem: The product of any family of compact spaces with the product topology is compact. This is equivalent to the Axiom of Choice.
If a space is both compact and Hausdorff then no finer topology on the space is compact, and no coarser topology is Hausdorff.

Some content on this page may previously have appeared on Citizendium.

Compact space

Contents

[edit] Cover and subcover of a set

[edit] Formal definition of compact space

[edit] Finite intersection property

[edit] Examples

[edit] Properties

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox