Commutative algebra
Commutative algebra developed as a theory in mathematics having the aim of translating classical geometric ideas into an algebraic framework, pioneered by David Hilbert and Emmy Noether at the beginning of the 20th century.
[edit] Definitions and major results
The notion of commutative ring assumes commutativity of the multiplication operation and usually also the existence of a multiplicative identity.
The category of commutative rings has
- commutative rings as its objects
- ring homomorphisms as its morphisms; i.e., functions
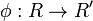such that 
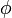is a morphism of abelian groups (with respect to the additive structure of the rings R andR'), 
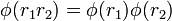for all 
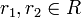, and 
.
[edit] Affine Schemes
The theory of affine schemes was initiated with the definition of the prime spectrum of a ring, the set of all prime ideals of a given ring. For curves defined by polynomial equations over a ring A, the object to consider would be the prime spectrum of a polynomial ring in sufficiently many variables modulo the ideal generated by the polynomials in question. The Zariski topology (together with a structural sheaf of rings) on this set endows a geometric structure for which many illuminating algebro-geometric correspondences manifest themselves. For example, for a noetherian ring A, primary decomposition of an ideal I translates exactly into a decomposition of the closed subset V(I) into irreducible components.
Formally speaking, the assignment of a ring A to its prime spectrum Spec(A) is functorial, and is in fact an equivalence (of categories) between the category of commutative rings and affine schemes. It is this mechanism, in addition to a number of correspondence theorems, which allows us to change between the language of algebra and geometry.
|
Some content on this page may previously have appeared on Citizendium. |
