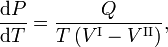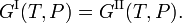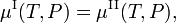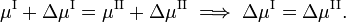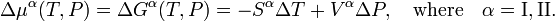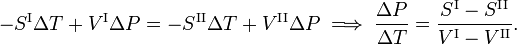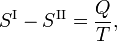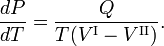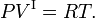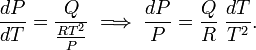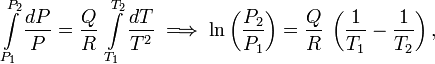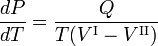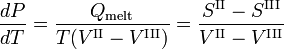Clausius-Clapeyron relation

From Knowino

Jump to: navigation, search

The red line in the P-T diagram is the coexistence curve of two phases, I and II, of a single-component system. Phase I may be the vapor and II the liquid phase of the component. The lower green line gives the slope in phase I and the upper green line in phase II.

The Clausius-Clapeyron relation is an equation for a single-component system^[1] consisting of two phases in thermodynamic equilibrium at constant absolute temperature T and constant pressure P. A curve in a two-dimensional thermodynamical diagram that separates two phases in equilibrium is known as a coexistence curve. The Clausius–Clapeyron relation gives the slope of the coexistence curve in the P-T diagram:

$\frac{\mathrm{d}P}{\mathrm{d}T} = \frac{Q}{T\,(V^{\mathrm{I}} - V^{\mathrm{II}})} ,$

where Q is the molar heat of transition. It is the heat necessary to bring one mole of the compound constituting the system from phase II into phase I; it is also known as latent heat. For phase transitions with constant P, it is the molar transition enthalpy. For instance, when phase II is a liquid and phase I is a vapor, then Q ≡ H_v is the molar heat of vaporization (also known as molar enthalpy of evaporation). Further, V^I is the molar volume of phase I at the pressure P and temperature T of the point where the slope is considered and V^II is the same for phase II.

The equation is named after Émile Clapeyron, who published it in 1834, and Rudolf Clausius, who put it on firm thermodynamic basis in 1850.

[edit] Derivation

The condition of thermodynamical equilibrium at constant pressure P and constant temperature T between two phases I and II is the equality of the molar Gibbs free energies G,

$G^{\mathrm{I}}(T,P) = G^{\mathrm{II}}(T,P). \,$

The molar Gibbs free energy of phase α (α = I, II) is equal to the chemical potential μ^α of this phase. Hence the equilibrium condition can be written as,

$\mu^{\mathrm{I}}(T,P) = \mu^{\mathrm{II}}(T,P), \;$

which holds everywhere along the coexistence (red) curve in the figure.

If we go reversibly along the lower and upper green line in the figure [the tangents to the curve in the point (T,P)], the chemical potentials of the phases, being functions of T and P, change by Δμ^I and Δμ^II, for phase I and II, respectively, while the system stays in equilibrium,

$\mu^{\mathrm{I}}+\Delta \mu^{\mathrm{I}} = \mu^{\mathrm{II}}+\Delta \mu^{\mathrm{II}} \;\Longrightarrow\; \Delta \mu^{\mathrm{I}} = \Delta \mu^{\mathrm{II}} .$

From classical thermodynamics it is known that

$\Delta \mu^{\alpha}(T,P) = \Delta G^{\alpha}(T,P)= -S^{\alpha} \Delta T +V^{\alpha} \Delta P, \quad\hbox{where}\quad \alpha = \mathrm{I, II}.$

Here S^α is the molar entropy (entropy per mole) of phase α and V^α is the molar volume (volume of one mole) of this phase. It follows that

$-S^{\mathrm{I}} \Delta T +V^{\mathrm{I}} \Delta P = -S^{\mathrm{II}} \Delta T +V^{\mathrm{II}} \Delta P \;\Longrightarrow\; \frac{\Delta P}{\Delta T} = \frac{S^{\mathrm{I}} - S^{\mathrm{II}}}{V^{\mathrm{I}} - V^{\mathrm{II}}}.$

From the second law of thermodynamics it is known that for a reversible phase transition it holds that

$S^{\mathrm{I}} - S^{\mathrm{II}} = \frac{Q}{T},$

where Q is the amount of heat necessary to convert one mole of compound from phase II into phase I. Elimination of the entropy and taking the limit of infinitesimally small changes in T and P gives the Clausius-Clapeyron equation,

$\frac{dP}{dT} = \frac{Q}{T(V^{\mathrm{I}} - V^{\mathrm{II}})} .$

[edit] Approximate solution

The Clausius-Clapeyron equation is exact. When the following assumptions are made, it may be integrated:

The molar volume of phase II is negligible compared to the molar volume of phase I: V^I >> V^II. In general, far from the critical point, this inequality holds well for liquid-gas equilibriums.

Phase I satisfies the ideal gas law, where R is the molar gas constant,

$PV^{\mathrm{I}} = R T. \,$

If phase I is a gas and the pressure is fairly low, this assumption is reasonable.

The transition (latent) heat Q is constant over the temperature integration interval. The integrations run from the lower temperature T₁ to the upper temperature T₂ and from P₁ to P₂.

Under these condition the Clausius-Clapeyron equation becomes

$\frac{dP}{dT} = \frac{Q}{\frac{RT^2}{P}} \;\Longrightarrow\; \frac{dP}{P} = \frac{Q}{R}\; \frac{dT}{T^2} .$

Integration gives

$\int\limits_{P_1}^{P_2} \frac{dP}{P} = \frac{Q}{R}\; \int\limits_{T_1}^{T_2} \frac{dT}{T^2} \;\Longrightarrow\; \ln\left(\frac{P_2}{P_1}\right) = \frac{Q}{R}\;\left( \frac{1}{T_1} - \frac{1}{T_2} \right),$

where ln(P₂/P₁) is the natural (base e) logarithm of P₂/P₁. We reiterate that for a gas-liquid equilibrium Q = H_v, the heat of vaporization.

For example, at the top of Mount Everest, atmospheric pressure is about a third of its value at sea level. Using the values R = 8.3145 J/K and Q = 40.65 kJ/mol, the equation gives T₂ = 1/[1/373.16 + 8.3145 ln(3) / (40.65 10³) ] = 344 K (71 °C) for the boiling temperature of water. It takes many hours to boil an egg on top of the Mount Everest in water of 71 °C.

[edit] Application

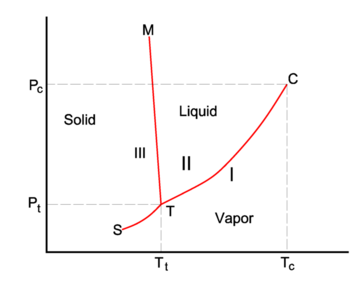
P-T diagram of water. Schematic and qualitative.

In the figure on the right an impression of part of the phase diagram of water (H₂O) is shown. The three phases are: I (vapor), II (liquid) and III (solid). The Clausius-Clapeyron equation

$\frac{dP}{dT} = \frac{Q}{T(V^\mathrm{I}-V^\mathrm{II})}$

gives the slope of the three coexistence (equilibrium, red) curves. The boiling line T-C has a positive slope, because the heat of vaporization Q = H_v is positive and the molar volume of the vapor V^I is (much) larger than that of the liquid V^II. For a similar reason the sublimation (transition from solid to vapor) line T-S has a positive slope. The sublimation line T-S is steeper than the boiling line T-C because the heat of sublimation is larger than the heat of vaporization, while in the neighborhood of crossing point T (the triple point) the difference in molar volumes is nearly equal. The melting line T-M has a negative slope, which occurs only for a few compounds (among them water). Consider

$\frac{dP}{dT} = \frac{Q_\mathrm{melt}}{T(V^\mathrm{II}-V^\mathrm{III})} = \frac{S^\mathrm{II}- S^\mathrm{III}}{V^\mathrm{II}-V^\mathrm{III}}$

The molar volume V^III of the solid is larger than the molar volume V^II of the liquid, while the enthalpy of melting Q_melt = S^II−S^III > 0 (a liquid has a larger entropy than the corresponding solid, it costs energy to melt a solid). Compounds that have melting lines with negative slope, have a solid phase of lower density than the liquid phase. For example, it is very well-known that solid water (ice) floats on liquid water.

The point C is the critical point. Beyond this point the vapor and the liquid are one indistinguishable fluid. There is no phase transition or a phase interface to the right of the melting line and above the line of constant P = P_c. The gas/liquid fluid also appears to the right of the line of constant T = T_c.

For water the critical point C is at (T_c, P_c) = (647.1 K, 220.6 bar) (a bar is almost equal to an atmosphere and is 100 kpascal) and the triple point T is at (T_t, P_t) = (273.16 K, 6.1173 mbar).

The Clausius-Clapeyron relation also holds for transitions between different crystalline phases.

[edit] Reference

↑ See J.C.M. Li, Clapeyron Equation for Multicomponent Systems, Journal of Chemical Physics, vol. 25, pp. 572–574 (1956) for a generalization to systems of more than one component.

[0] See J.C.M. Li, Clapeyron Equation for Multicomponent Systems, Journal of Chemical Physics, vol. 25, pp. 572–574 (1956) for a generalization to systems of more than one component.

[1]

Clausius-Clapeyron relation

Contents

[edit] Derivation

[edit] Approximate solution

[edit] Application

[edit] Reference

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox