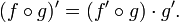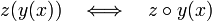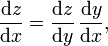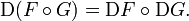Chain rule

From Knowino

This is a pending revision of this page. It may differ from the latest accepted revision, which was accepted on 13 January 2011.

Pending changes are displayed on this page

Jump to: navigation, search

In calculus, the chain rule describes the derivative of a "function of a function": the composition of two function, where the output z is a given function of an intermediate variable y which is in turn a given function of the input variable x.

Suppose that y is given as a function 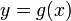$\,y = g(x)$ and that z is given as a function 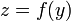$\,z = f(y)$ . The rate at which z varies in terms of y is given by the derivative 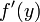$\, f'(y)$ , and the rate at which y varies in terms of x is given by the derivative 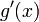$\, g'(x)$ . So the rate at which z varies in terms of x is the product 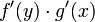$\,f'(y)\sdot g'(x)$ , and substituting 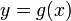$\,y = g(x)$ we have the chain rule

$(f \circ g)' = (f' \circ g) \sdot g' . \,$

In order to convert this to the traditional (Leibniz) notation, we notice

$z(y(x))\quad \Longleftrightarrow\quad z\circ y(x)$

and

$(z \circ y)' = (z' \circ y) \sdot y' \quad \Longleftrightarrow\quad \frac{\mathrm{d} z(y(x))}{\mathrm{d} x} = \frac{\mathrm{d} z(y)}{\mathrm{d} y} \, \frac{\mathrm{d} y(x)}{ \mathrm{d} x} . \,$ .

In mnemonic form the latter expression is

$\frac{\mathrm{d} z}{\mathrm{d} x} = \frac{\mathrm{d} z}{\mathrm{d} y} \, \frac{\mathrm{d} y}{ \mathrm{d} x} , \,$

which is easy to remember, because it as if dy in the numerator and the denominator of the right hand side cancels.

[edit] Multivariable calculus

The extension of the chain rule to multivariable functions may be achieved by considering the derivative as a linear approximation to a differentiable function.

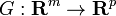Now let $F : \mathbf{R}^n \rightarrow \mathbf{R}^m$ and $G : \mathbf{R}^m \rightarrow \mathbf{R}^p$ be functions with F having derivative $D F$ at $a \in \mathbf{R}^n$ and G having derivative $D G$ at $F(a) \in \mathbf{R}^m$ . Thus $D F$ is a linear map from 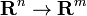$\mathbf{R}^n \rightarrow \mathbf{R}^m$ and $D G$ is a linear map from 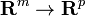$\mathbf{R}^m \rightarrow \mathbf{R}^p$ . Then $F \circ G$ is differentiable at $a \in \mathbf{R}^n$ with derivative