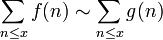Average order of an arithmetic function

In mathematics, in the field of number theory, the average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".

Let f be a function on the natural numbers. We say that the average order of f is g if

as x tends to infinity.

It is conventional to assume that the approximating function g is continuous and monotone.

[edit] Examples

• The average order of d(n), the number of divisors of n, is log(n);
• The average order of σ(n), the sum of divisors of n, is ;
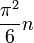• The average order of φ(n)), Euler's totient function of n, is ;
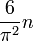• The average order of r(n)), the number of ways of expressing n as a sum of two squares, is π ;
• The Prime Number Theorem is equivalent to the statement that the von Mangoldt function Λ(n) has average order 1.

[edit] See also

• Divisor function
• Normal order of an arithmetic function

[edit] References

• G.H. Hardy; E.M. Wright (2008). An Introduction to the Theory of Numbers, 6th ed.. Oxford University Press, 347-360. ISBN 0-19-921986-5. 
• Gérald Tenenbaum (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press, 36-55. ISBN 0-521-41261-7. 

Some content on this page may previously have appeared on Citizendium.